Г и п е р б о л а

Гиперболой называется геометрическое место точек на плоскости, для каждой из которых абсолютная величина разности расстояний до двух данных точек F₁, F₂, называемых фокусами гиперболы, есть величина постоянная, равная 2а и меньшая, чем расстояние между фокусами 2с.

Выведем уравнение гиперболы, исходя из данного определения.

Выберем систему координат так, чтобы ось абсцисс проходила через фокусы гиперболы F₁ и F₂. Ось ординат проведем через середину отрезка перпендикулярно F₁ F₂ ему.

Пусть M(x,y) - произвольная точка гиперболы. Расстояния от любой точки M(x,y) гиперболы до фокусов называются ее фокальными радиусами.

r₁ =F₁M; r₂=F₂M – фокальные радиусы.

Согласно определению гиперболы . Тогда координаты точек гиперболы удовлетворяют уравнению

, или ,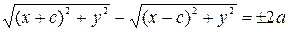

где знак «плюс» соответствует случаю, когда левая часть уравнения положительна, а знак «минус» соответствует противоположному случаю. Уединяя один из радикалов, возводим обе части уравнения в квадрат:

,

,

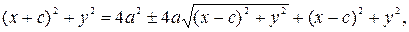
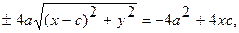
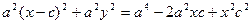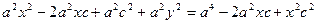
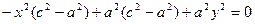
По определению гиперболы разность а<с, поэтому разность 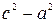положительное число. Обозначим с² – а² = b². После деления на уравнение примет вид:

Это уравнение называется каноническим уравнением гиперболы.

Установим форму гиперболы по ее каноническому уравнению.

Из уравнения 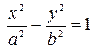видно, что гипербола симметрична относительно осей OX, OY и начала координат О(0;0), так как вместе с точкой (x,y) ей принадлежат и точки (-x,-y), (-x, y), (x, -y). Точка О(0;0) называется центром гиперболы.

Найдем точки пересечения гиперболы с осями координат.

С осью Ох: .

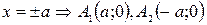С осью Оу: чего быть не может. Следовательно, гипербола ось Оу не пересекает.

Точки 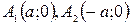называются вершинами гиперболы. Отрезок называется действительной осью гиперболы, а отрезок 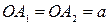- действительной полуосью гиперболы.

Дата добавления: 2014-01-05