Фаззі-керування електроприводами

В розділі 8 розглянуті дискретні логічні системи керування елек-троприводами, які побудовані за класичною логікою, що оперує з фізичними величинами двох рівнів (високий-низький, одиниця-нуль) і дозволяє успішно реалізувати нескладні алгоритми керуван-ня. Для підвищення точності і плавності керування багатьма склад-ними, особливо нелінійними об’єктами, необхідно знати не лише два крайні рівні керованих величин, але і проміжні, а також закони переходу від одного рівня до іншого. Наприклад, на запитання, чи рухається автомобіль, можна відповісти однозначно «так» чи «ні». Але на запитання, як рухається автомобіль (дуже повільно, повіль-но, швидко, дуже швидко) дворівнева логіка не дає відповіді. Для опису таких задач використовують фаззі-логіку, розроблену амери-канським професором електротехніки Л. Заде.

Математичною основою фаззі-логіки є фаззі-множина (ФМ), яка характеризується двома показниками: фактом належності до даної множини, як у класичній логіці - 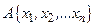, і ступенем належ - ності до неї 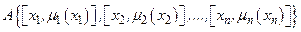Сто-совно систем керування елементами ФМ є певний діа-пазон значень фізичної змінної, наприклад, переміщення, швидкос-ті, струму, температури тощо. Лінгвістичне представлення фізичної змінної називається логічною змінною в фаззі-логіці. Властивістю, яка об’єднує значення фізичної змінної в ФМ, є певна якісна оцінка у лінгвістичній формі логічної змінної, наприклад, від’ємнo мала (NS), нульова (Z), позитивно середня (PM), позитивно велика (PB) та ін. Ці якісні оцінки називаються термами. Ступінь належності значень фізичної змінної до даного терму називається функцією належності (ФН) і позначається .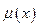

Фізична величина 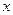на заданому інтервалі її зміни від 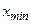до 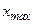поділяється на ФМ (терми) 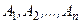з функціями належ-ності 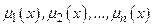. Кількість термів та вид ФН визначає досвідчений оператор, користуючись відповідною процедурою прийняття рішень.

Для кращого розуміння фаззі-керування розглянемо методику побудови й функціонування на прикладі системи регулювання температури у приміщенні (рис.14.5). Об’єктом керування ОК є приміщення, температура в якому регулюється електрокалорифером ЕК, що живеться від регульованого джерела напруги РДН, який керується фаззі-регулятором ФР.

Рис.14.5. Структурна схема системи фаззі-керування

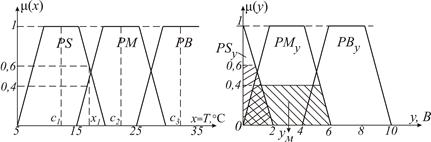
Нехай експерт приймає рішення, що температура у приміщенні може змінюватись від 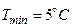до 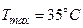, яку представляє трьома термами: позитивно низька (PS) для 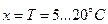; пози-тивно середня (PM) для 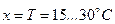і позитивно висока (PB) для 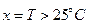у виді трапецій з функціями належност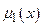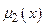і , і 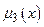та з центрами 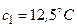, 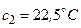і 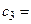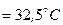(рис.14.6,а).При цьому експерт-медик рахував, що темпе-ратура 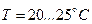найбільше комфортна для людини і вона прийнята за середню, 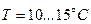є беззаперечно низька, коли потрібно значно посилити подачу тепла кондиціонером, а 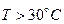– беззаперечно висока і потрібно перевести кондиціонер в режим охолодження:

а б

Рис.14.6. Приклади фаззі-множин і функцій приналежності

Суть фаззі-логіки в її нечіткості, яка визначається ділянками перекриття термів. Форма термів, їх кількість і перекриття можуть бути різними, але умова перекриття така: де для одного терма 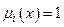, для сусідніх .

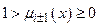Чим складніша форма терма й чим їх більше, тим складніша про-цедура визначення керуючого впливу і тим вища точність керуван-ня, але зменшується швидкодія, бо збільшується час логічних пере-творень.

В зоні перекриття вхідна змінна 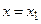(рис.14.6, а) відноситься до двох термів зі ступенями належності 0,6 і 0,4 і тому виникає проблема, як цю двозначність перетворити у чіткий вихідний сигнал. Цю проблему вирішує фаззі-регулятор на основі принципів су-міщення нечітких множин (термів). Процес перетворення інформа-ції у ФР складається з трьох етапів: фаззіфікації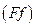, логічного висновку 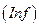і дефаззіфікації 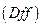(рис. 14.7).

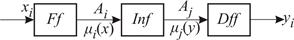
Рис. 14.7. Структурна схема фаззі-регулятора

Фаззіфікація – це процедура визначення належності вхідного сигналу 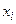до відповідного терма 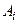чи до суміжних з функцією належності 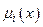, яка реалізується блоком .

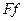Логічний висновок 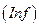– це визначення (активізація) за виб-раними (активізованими) термами 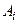термів 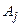вихідної лінгвіс-тичної змінної й присвоєння їм згідно принятих процедур фаззі-логіки ФН 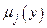. Для цього експерт встановлює необхідні межі керуючого впливу 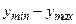та терми, кількість яких повинна бути не менша кількості термів .

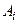Стосовно регулювання температури у приміщенні нехай експерт визначає, що 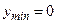і 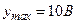, і цей інтервал представляє трьома термами (рис. 14.6,б) за такою фаззі-логікою: якщо темпера-тура у приміщенні низька (терм PS), то йому відповідає вихідний терм PB_у – нагрівати приміщення треба сильно. Аналогічно встано-влюється зв'язок між іншими термами, що у термінах фаззі-логіки має вид:

якщо PM, то PM_у;

якщо PB, то PS_у.

Коли вхідна змінна відноситься до двох термів зі ступенем на-лежності 0,6 і 0,4 (див. рис.14.6,а), то для логічних зв’язків типу «І» активізовані вихідні терми PS_у і PM_у зрізаються на рівнях 0,6 і 0,4, як показано на рис. 14.6,б. Результатом логічного висновку для 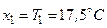буде заштрихована фігура, яка складається зі зрі-заних трикутника і трапеції. Вона являє собою нечітку множину (об’єднаний терм), яку потрібно перетворити в однозначний вихід-ний сигнал за допомогою процедури дефаззіфікації.

Дефаззіфікація – це процедура розрахунку за нечіткою множи-ною – логічним висновком – чіткого сигналу фаззі-регулятора. Є різні методи дефаззіфікації. Один з них – це обчислення проекції на вісь у центра маси фігури–логічного висновку – за формулою

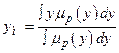, (14.12)

де 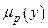– ломана лінія, що обмежує зрізані площі активізованих термів. Обчислена за (14.12) вихідна змінна 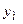і є керуючим впли-вом для вхідної змінної .

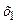Аналіз впливу форми термів, їх кількості і ширини зони перек-риття показує, що трикутна форма термів з перекриттям 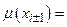формує вихідну характеристику ФР подібну до характеристик аналогових регуляторів з обмеженням, а звуження зони перекриття призводить до підвищення коефіцієнта підсилення. Трапецієвидні терми спричиняють східчасту форму вихідної характеристики 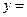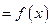. Використання нерівнобоких термів дозволяє сформувати будь-яку нелінійну залежність .

Фаззі-регулятори часто мають не одну вхідну змінну, а декілька. У цьому випадку процедура підбору термів не змінюється, але збі-льшується обсяг логічних перетворень і число правил, за якими во-ни здійснюються. Досвід показує, що достатньо вхідні змінні пред-ставляти п’ятьма термами кожну, а вихідну – сьома. При цьому най-менший обсяг обчислень буде у випадку рівнобедрених трикутних термів.

Слід відмітити, що фаззі-керування:

Ø не потребує знання точної моделі об’єкта, оскільки воно реалізує наближену стратегію керування, моделюючи процес мислення людини;

Ø дозволяє створювати широке коло лінійних і нелінійних алгоритмів керування;

Ø забезпечує високу надійність завдяки дискретному характе-ру роботи ФР;

Ø просте в реалізації на базі мікропроцесора.

У зв’язку з наведеним фаззі-керування є дуже перспективним на-прямом побудови досконалих систем керування рядом електропри-водів, використовуючи для цього пакети програм Fuzzy Logic Tool-box програмного пакету Matlab.

Дата добавления: 2014-01-05