Диффузия в среде со сферической симметрией

Распределение концентрации С вещества, диффундирующего в сферически-симметричном слое, определяется выражением

,

где:

С₁ – концентрация на внутренней границе сферического слоя (r = r₁) в течение всего времени диффузии;

С₂ – концентрация на внешней границе сферического слоя (r = r₂) в течение всего времени диффузии. Эту формулу используют при больших значениях t (точнее, больших параметрических числах Фурье Dt/(r₁ – r₂)². При (Dt/(r₁ – r₂)²) << 1 удобнее пользоваться выражением

,

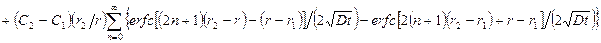где:

erfc означает 1 – erf.

Количество вещества, поглощенного или выделенного за время t в процессе диффузии из сферически-симметричного слоя при нулевой начальной концентрации (С₀ = 0) и при больших значениях t, определяется выражением

.

При малых диффузионных числах Фурье количество поглощенного диффундирующего вещества рассчитывается по более удобной формуле

,

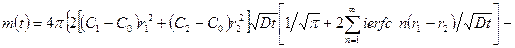
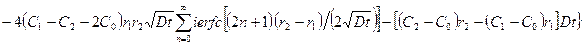где:

.

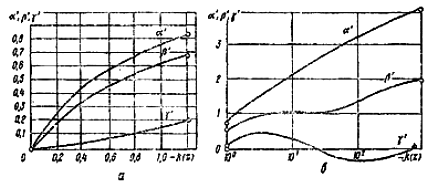
Рис. 4.6. Зависимость коэффициентов a¢, b¢, g¢ от параметра k(z) при малых (а) и при

больших (б) значениях k(z)

При униполярном растворении сферического включения, когда диффузия внутри его пренебрежимо мала и его растворение определяется диффузией в матрице неограниченных размеров, изменение относительных размеров включения во времени описывается рядом , где r₀ и r – соответственно начальный и текущий радиус включения; a¢, b¢, g¢ – безразмерные коэффициенты; – безразмерное время. Предполагается, что на поверхности включения сохраняется равновесная для данной температуры концентрация С₁, определяемая из диаграммы состояния. Начальный радиус включения r₀, текущий радиус – r(t). Вдали от включения сохраняется исходная концентрация С₀, т. е, 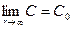. Непосредственно у поверхности сферической частицы С (r(t), t) = С₁. Начальное условие С (r, 0) = С₀.

Коэффициенты a¢, b¢, g¢ являются функцией одного параметра k(z) = (C₁ – C₀)/(C₁ – C₂) (рис. 4.6).

Дата добавления: 2014-01-05