Relative velocity

INERTIAL REFERENCE FRAMES

The position or velocity of a particle has meaning only in relation to other bodies. When told the speed of a car, we all assume that it was measured relative to the road. The road is an example of a reference frame. A reference frame is something physical, such as a road, a train, a tabletop, or even the earth itself. A reference frame in which Newton's first law is valid is called an inertial reference frame. In fact, the first law is used to define such a frame:

In an inertial reference frame, a body subject to no net force will either stay at rest or move at constant velocity.

Any frame moving at constant velocity relative to a known inertial frame is also an inertial frame. If the acceleration of a particle is zero in one inertial frame, it is zero in all inertial frames.

Because of the daily rotation of the earth, a frame based on its surface is continually changing the direction of its velocity. Hence, it is not really an inertial frame. Even if the earth were not rotating, it would still be in orbit around the sun, which itself has an acceleration relative to other stars. Our innocent little definition of an inertial frame has led us into quicksand. We have developed Newton's first law and the concept of an inertial frame without ever having direct experience with one.

All is not lost, however. The acceleration of an object at the surface of the earth, and the earth's acceleration in its orbit around the sun, are quite small. For experiments conducted over a small area, such as a laboratory, a frame based on the surface of the earth is a perfectly adequate approximation to an inertial frame. For interplanetary travel, a frame based on the sun or nearby stars serves us very well. To the question of whether there is a "real" inertial frame, there is no clear-cut answer. Newton proposed that a frame based on the "fixed stars" could serve as the standard inertial frame. This is as good as we are ever likely to need.

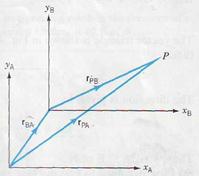
FIGURE 3.1

The motion of any body has to be described relative to some frame of reference, such as the ground. Sometimes it is necessary to examine the motion of one body relative to another body that is also moving relative to the ground. For one-dimensional motion, it is easy to determine the velocity of one body relative to another. Consider car A which is moving north at 35 m/s and is ahead of car B, which is moving north at 30 m/s. These velocities are relative to the ground. Relative to observers in car B, car A is moving north at 5 m/s, whereas relative to car A, car В is moving south at 5 m/s. We now consider how to determine relative motion in two dimensions.

In Fig. 3.1 the position of a particle P with respect to frame A is r _PA. The position of P with respect to frame В is r _PB. Finally, the position of frame В with respect to frame A is r _ВA. The vector triangle shows that

r_PA= r_PB + r_BA (3.1)

Now suppose both the particle P and the frame В are moving with respect to frame A. Since v = d r /dt, Eq. 3.1 leads to

v _PA = v _PB + v _BA (3.2)

Notice that Eq. 3.2 is a vector sum —we worry about signs only when we take components. The order of the subscripts should be carefully noted. In general,

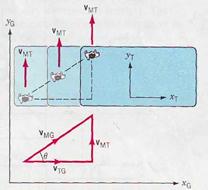
FIGURE 3.2

v _AB = − v _BA (3.3)

Let us consider a concrete example. In Fig. 3.2 a man walks across a train with velocity v _MT, relative to the train. The train itself moves relative to the ground with velocity v _TG. The ground forms a stationary frame (x _G, y _G), while the train forms a moving frame (x _T, y _T). We wish to find the velocity of the man

relative to the ground, that is, v _MG. From Eq.3.2 we have

v _MG = v _MT + v _TG

An observer on the train will see the man walk along the y _T axis. An observer on the ground will see him move in a direction given tan θ = by to the x _G axis.

Дата добавления: 2014-01-05