Mass versus Weight

WEIGHT

Mass

Newton defined mass as the "quantity of matter" in a body. This expresses an intuitive feeling, but is not useful. How, for example, are we to compare quantities of matter? Newton's first law provides the clue to a better definition:

FIGURE 3.7

The mass of a body is a measure of its inertia, that is, its resistance to change in velocity.

The mass of a body is a scalar quantity that tells us how difficult it is to change the magnitude, or direction, of its velocity. Mass is an intrinsic property of a body, independent of its location.

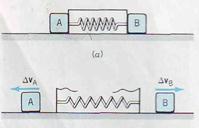
To compare the masses of two pucks, we place them on a table. The pucks are then placed on either side of a spring that is held in a compressed state by a thread, as shown in Fig. 3.7 a. When the thread is cut, the pucks are pushed apart and undergo changes in velocity ∆ v _A and ∆ v _B, shown in Fig. 3.7 b. We discover that for any time interval, the ratio |∆ v _A|/|∆ v _B| is a fixed number for the two given pucks. The nature of the interaction does not matter. They can interact via the spring, via magnets attached to them, or directly with each other as in a collision. Since mass is a measure of resistance to change in velocity, we define the ratio of the masses to be

m _A/ m _B = |∆ v _B|/|∆ v _A| (3.8)

Once the standard kilogram has been chosen, we may in principle determine the mass of any other body.

3.6 NEWTON'S SECOND LAW

FIGURE 3.8

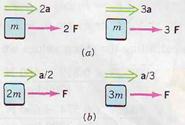
From Newton's first law we know that a net force acting on a body will produce an acceleration. To determine how the acceleration depends on the force and the mass of the body, these quantities must be varied one at a time. When the mass is held fixed and the force is varied, we find that acceleration is proportional to the force. When the force is kept constant and the mass is varied, we find that acceleration is inversely proportional to the mass. These results, depicted in Fig.3.8, tell us that a ≈ F / m. We conclude that F = kma, where k is a constant of proportionality. In SI units, a force of one newton (N) applied to mass of 1 kg produces an acceleration of 1 m/s², so k = 1:

1 N = 1 kg·m/s²

When several forces act on a particle, we must take their vector sum, so Newton's second law of motion is written as

∑ F = m a (3.9)

The net force, ∑ F, acting on a particle of mass m produces an acceleration a = ∑ F / m in the direction of the net force.

Equation 3.9 is equivalent to three equations in terms of the components:

∑ F _x= ma _x ∑ F _y= ma _y ∑ F _z= ma _z (3.10)

We now that the acceleration of a body is the same in all inertial reference frames. Since ∑ F = m a, Newton's second law of motion has the same form in all inertial frames.

3.7 NEWTON'S THIRD LAW

When you push against a wall, or pull at it, you experience a force in the opposite direction. The harder you push (or pull), the harder the wall pushes (or pulls) back. In fact, the force exerted by the wall on you is exactly equal in magnitude and opposite in direction to the force exerted by you on the wall. This is an example of Newton's third law, the law of action and reaction

F _AB = − F _BA. (3.11)

The force exerted on A by В is equal and opposite to the force exerted on В by A.

Notice that a force is exerted by one body on another; one should not refer to the force of a body. The third law says that there is no such thing as an isolated force; forces always occur in pairs.

The popular expression "To every action there is an equal and opposite reaction" does not emphasize that the forces act on different bodies. It is a bit startling to realize that an apple pulls the earth just as hard as the earth pulls the apple. Because of its obvious motion when dropped, it seems that only the apple is affected by the force of gravity. However, since the equal and opposite forces act on different bodies, the consequences of the forces may be vastly different. (When someone steps on your toes, it really does not help to know that your toes exerted an equal and opposite force on the other person's shoe.)

The third low is valid only in inertial frames, although the interacting particles themselves may be accelerating. This is equivalent to saying that it deals only with real forces associated with the basic interactions.

FIGURE 3.9

As part of an attempt to explain the motion of the planets around the sun, in 1687 Newton put forward a law of universal gravitation. It states that between any two point particles with masses m and M, separated by a distance r as in Fig. 3.9 a. there is an attractive force whose magnitude is given by

Newton’s law of gravitation 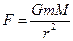(3.12)

where G = 6.67 ×10⁻¹¹ N·m²/kg²

The weight of an object is the net gravitational force acting on it.

It turns out that for the special case of a body whose mass distribution is spherically symmetric (a spherical shell or a solid sphere), Eq.3.12 may be used with r taken as the distance to the center. Thus, if the earth is taken to be a uniform sphere of mass M _E and radius R _E, as in Fig. 3.9 b, the weight of an object of mass m at its surface is

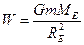(3.13)

This equation is usually written in the form

W = m g, (3.14)

where g = GM _E /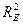, measured in N/kg, is the magnitude of the gravitational force per unit mass on an object at the surface and is called the gravitational field strength at the surface. Since W = mg has the same form as F = ma and the unit N/kg reduces to m/s², g is often called the "acceleration due to gravity".

The concepts of mass (a measure of the inertia of a body) and weight (the net gravitational force on a body) are often confused. The commercial and industrial use of the kilogram as a unit of weight further complicates the issue. The first point to note is that mass is a scalar measured in kilograms, whereas weight is a vector measured in newtons. Second, whereas mass is an intrinsic property that does not change with position, the weight of a body depends on the local value of g, which varies because of the nonspherical shape of the earth, oil and mineral deposits, altitude, and so on. If a body were taken to the moon, its weight would be only one-sixth of its value on earth. In outer space, far from any stars or planets, it would be essentially weightless. However, if we were to kick the body in its weightless state, it would still hurt our toes. Its mass, that is, its resistance to change in velocity, would not have changed.

Дата добавления: 2014-01-05