Springs

In Fig. 5.2 a, a block of mass m on a frictionless surface, is attached to a spring that is initially extended to x = A and then released. The force exerted by the spring will accelerate the block toward the equilibrium position x = 0. At an arbitrary point, the energy of the block-spring system is

E = 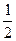mυ²+

and the conservation of mechanical energy states

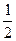mυ_f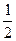²+= mυ_i²+

FIGURE 5.2

At its initial point there is no kinetic energy and the system has its maximum potential energy: E = K + U = 0 + ¹/₂ kA ². As the block speeds up and moves toward the origin, the gain in kinetic energy exactly balances the loss in potential energy so that their sum stays constant. At x = 0, the block has its maximum kinetic energy and zero potential energy, or E = K + U = ¹/₂ mυ ²_max + 0. In summary,

E=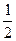mυ²+= 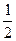mυ ²_max = (5.6)

Assuming that the coils of the spring do not touch, the block continues its motion past x = 0. Its kinetic energy decreases as its potential energy increases, until finally at x = −A the energy is again purely potential: E = K + U = 0 + ¹/₂ kA ². The variation of the kinetic and potential energies is shown in Fig. 5.2 b. Since the force due to the spring is always directed toward the origin, the block oscillates back and forth. The turning points are at x = ±A, where К = 0 and E = U _max.

Дата добавления: 2014-01-05