Общие сведения. Технические реализации. Применения

Технические реализации. Применения

Асинхронный двигатель с короткозамкнутым ротором уже около 100 лет используется и будет использоваться как практически единственная реализация массового нерегулируемого электропривода, составляющего до настоящего времени более 90% всех промышленных электроприводов. В последние 10-20 лет многими фирмами в Америке и Европе предпринимают попытки разработки и выпуска на широкий рынок так называемых энергоэффективных двигателей, в которых за счет увеличения на 30% массы активных материалов на 1 - 5% повышен номинальный КПД при соответствующем увеличении стоимости. В последние годы в Великобритании осуществлен крупный проект создания энергоэффективных двигателей без увеличения стоимости.

В последнее десятилетие благодаря успехам электроники (преобразователи частоты) короткозамкнутый асинхронный двигатель стал основой частотно-регулируемого электропривода, успешно вытесняющего доминировавший ранее электропривод постоянного тока во многих сферах. Особенно интересным является применение такого электропривода в традиционно нерегулируемых насосах, вентиляторах, компрессорах. Как показывает опыт, это техническое решение позволяет экономить до 50% электроэнергии, до 20% воды и более 10% тепла.

Переход от нерегулируемого электропривода к регулируемому во многих технологиях рассматривается как основное направление развития электропривода, поскольку при этом существенно повышается качество технологических процессов и экономится до 30% электроэнергии. Это определяет перспективы развития частотно-регулируемого электропривода.

Электропривод с двигателями с фазным ротором при реостатном регулировании традиционно находит широкое применение в крановом хозяйстве, используется в других технологиях. Каскадные схемы и машины двойного питания можно встретить в мощных электроприводах газоперекачивающих станций с небольшим диапазоном регулирования, в устройствах электродвижения судов. Синхронные двигатели до недавнего времени использовались относительно редко - главным образом в мощных установках, где не требовалось регулирование скорости. В последние годы положение существенно изменилось: за счет современных материалов (постоянные магниты), средств управления (ключи на относительно большие токи и напряжения и т.д.) Электропривод с синхронными двигателями стал управляемым, существенно расширился диапазон мощностей и занял ведущие позиции в станкостроении, робототехнике, гибких производственных системах и т.п.

Свойство синхронной машины с обмоткой возбуждения менять реактивную мощность и ее знак позволяет использовать ее как управляемый компенсатор реактивной мощности.

Предельная простота, надежность и низкая стоимость вентильно-индукторной машины и электропривода в целом, а также его широкие функциональные возможности и высокие энергетические показатели позволяют считать этот тип электропривода наиболее перспективным регулируемым электроприводом для широких промышленных и транспортных применений.

Как отмечалось, практически единственным рациональным способом регулирования скорости асинхронных двигателей с к.з. ротором и синхронных двигателей является изменение частоты питающего напряжения.

Большинство современных преобразователей частоты (ПЧ) от долей кВт до сотен кВт построены одинаково - рис. 4.15: сеть переменного тока - неуправляемый выпрямитель В - шины постоянного тока - конденсатор LC -фильтра - автономный инвертор напряжения И с широтно-импульсной модуляцией (ШИМ) - асинхронный двигатель АД, к которому приложено переменное 3-фазное напряжение с регулируемой частотой f = var и амплитудой U = var; управление инвертором осуществляется блоком управления БУ.

Рис. 4.15. Типовая схема преобразователя частоты

Идею автономного инвертора напряжения (АИН) проиллюстрируем на простейшей однофазной схеме с четырьмя идеальными ключами 1, 2, 3, 4 и активной нагрузкой R - рис. 4.16,а.

При попарной коммутации ключей 1,2 - 3,4 - 1,2 и т.д. через время Т/2 (рис. 4.16,б) к резистору будет прикладываться переменное напряжение u_ab прямоугольной формы с частотой 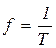. Ток при активной нагрузке будет повторять форму напряжения. Изменяя коммутационный промежуток Т/2, можно менять частоту в любых пределах.

а)

б)

Рис. 4.16. Однофазный инвертор, нагруженный активным сопротивлением (а), и диаграмма работы (б)

При активно-индуктивной нагрузке размыкание ключа недопустимо без дополнительных мер, поскольку энергия, запасенная в индуктивности, при разрыве цепи вызовет большие пики перенапряжений и сделает устройство полностью неработоспособным. Следовательно, при размыкании ключей должны оставаться контуры, по которым продолжал бы протекать ток в прежнем направлении и запасалась бы энергия, переданная из разряжающейся индуктивности.

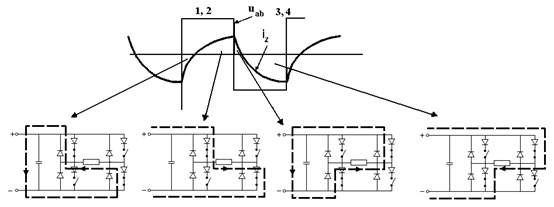
Конфигурация схемы, при которой выполняются указанные условия, показана на рис. 4.17,а. Пунктирные диоды у ключей 1-4 отражают их одностороннюю проводимость. Диоды D1 - D4 образуют вместе с конденсатором С контуры для обмена энергией. Коммутация ключей не отличается от показанной на рис. 4.16, однако ток на каждом полупериоде меняет направление, протекая по контурам, показанным на рис. 4.17,б. Нетрудно видеть, что формы напряжения и тока существенно различны, и ток в силу индуктивного характера нагрузки отстает от напряжения.

а)

б)

Рис. 4.17. Однофазный инвертор с R – L нагрузкой (а) и диаграмма работы (б)

Рассмотренные выше принципы построения и работы однофазных автономных инверторов напряжения легко распространяются на m-фазные (обычно - трехфазные) схемы.

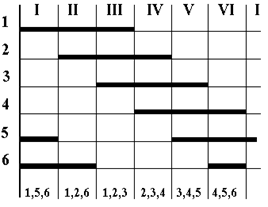
Трехфазным аналогом однофазной схемы (рис. 4.16,а) будет схема, приведенная на рис. 4.18,а, имеющая шесть ключей 1, 2, 3, 4, 5, 6. Мы, как и прежде, рассматриваем идеализированный случай, полагая для простоты, что соединенные в звезду сопротивления нагрузки - активные. Для количественных оценок примем U = 1 и R_А=R_В=R_С=R=1.

а) б)

Рис. 4.18. Схема трехфазного инвертора (а) и диаграмма коммутации (б)

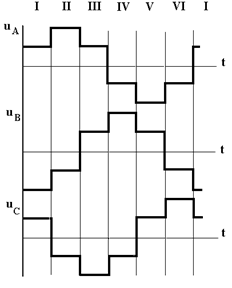
Разделим период выходного напряжения на шесть интервалов I - VI и условимся коммутировать ключи в начале каждого интервала в порядке их номеров, указанных на рис. 4.18,а. В результате получим диаграмму коммутации, показанную на рис. 4.18,б. Здесь принята так называемая 180° коммутация, т.е. каждый ключ, замкнувшись, продолжает оставаться включенным три интервала, т.е. 1/2 периода или 180°. Включенное состояние ключей отмечено на диаграмме жирными линиями; внизу указанно, какие из ключей замкнуты на каждом интервале.

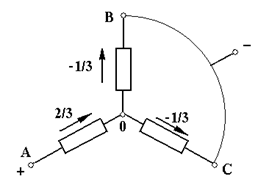
На интервале I точки А и С связаны с “плюсом” источника, а точка В с “минусом”, т.е. интервалу I соответствует схема на рис. 4.19,а. Нетрудно видеть, что сопротивление цепи между “+” и “-” составит при принятых величинах 1/2+1=3/2, общий ток будет 1:3/2=2/3, тогда фазные напряжения на I интервале будут: U_AI = 1/3, U_BI = -2/3 и U_CI = 1/3 (положительным принято направление от зажимов А,В,С - к нулю). Если перейти к векторному представлению величин, то получим диаграмму на рис. 4.19,б: результирующий вектор, равный 1, направлен по оси фазы В.

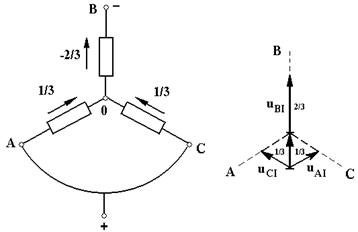
Рис. 4.19. Диаграммы токов (а) и напряжений (б) на интервале I

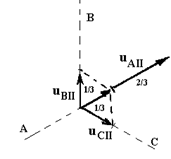
Рассмотрим аналогично интервал II. Здесь точка А связана с “+”, а точки В и С - с “-” - схема на рис. 4.20,а. Аналогичными рассуждениями получим фазные напряжения: U_AII = 2/3, U_BII = -1/3 и U_CII = -1/3, векторная диаграмма - на рис. 4.20,б. Результирующий вектор, попрежнему равный 1, сместится по часовой стрелке на 60°.

а) б)

Рис. 4.20. Диаграммы токов (а) и напряжений (б) на интервале II

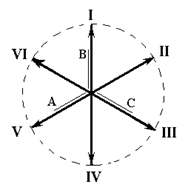
Повторяя подобные рассуждения для остальных интервалов, получим диаграммы фазных напряжений на рис. 4.21,а и векторную диаграмму на рис. 4.21,б. Иногда вместо 180° коммутации используют 120° коммутацию, когда каждый ключ замкнут на протяжении двух интервалов. Нагрузка может быть при любой коммутации включена как в звезду, так и в треугольник. В этих вариантах будут несколько изменяться формы напряжений и их амплитуды, но принцип получения трехфазных (в общем случае - m -фазных) напряжений останется неизменным. При активно-индуктивной нагрузке останутся в силе рассмотренные ранее в однофазном варианте необходимые добавления - диоды, которые шунтируют ключи, и конденсатор, участвующий в процессе перекачки запасаемой в индуктивностях энергии на каждом такте работы схемы.

а) б)

Рис. 4.21. Диаграммы фазных напряжений

Изложенный принцип преобразования постоянного напряжения в переменное, основанный на использовании управляемых ключей, в различных модификациях и вариантах используется в подавляющем большинстве современных преобразователей частоты. В частности, он используется в автономных инверторах тока, когда на входе инвертора включен реактор, индуктивность которого достаточна для поддержания тока нагрузки практически неизменным в течение полупериода выходной частоты. Таким образом, в АИТ задается мгновенное значение тока, он питается от источника тока. Напряжение - зависимая переменная. Обычно нагрузка шунтируется конденсатором в целях создания условий коммутации ключей - тиристоров - и обеспечения нормальной работы при активно-индуктивной нагрузке.

Из изложенного следует, что управляемые ключи позволяют преобразовывать постоянное напряжение в m - фазное переменное напряжение нужной частоты, однако остался открытым вопрос об управлении амплитудой переменного напряжения. Принципиально есть несколько возможностей. Первая - и очевидная - использовать для связи с сетью управляемый выпрямитель взамен неуправляемого. Эта возможность используется обычно в АИТ и в последнее время в некоторых АИН для обеспечения рекуперации энергии в сеть и снижения вредного влияния инвертора на сеть. Вторая возможность - варьирование длительности импульса внутри каждого полупериода. Третья, повсеместно используемая в современных преобразователях частоты на основе АИН, - широтно-импульсная модуляция ШИМ.

Идею построения автономного инвертора напряжения с ШИМ проиллюстрируем на простейшей идеализированной однофазной схеме с чисто активной нагрузкой - рис. 4.16,а.

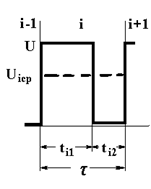
Для изменения амплитуды и формы напряжения на нагрузке раздробим каждый период Т на n равных частей (интервалов) с продолжительностью каждого 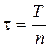и будет коммутировать ключи 1,2 на каждом интервале положительного полупериода, а ключи 3,4 - на каждом интервале отрицательного полупериода как показано на рис. 4.22,а. Тогда на каждом интервале i к нагрузке будет прикладываться не полное напряжение U, а лишь его часть U_iср:

.

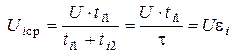а) б)

Рис. 4.22. ШИМ на интервале (а) и на половине периода выходной частоты (б)

Меняя на каждом интервале относительную ширину импульса ,

можно легко управлять средним за интервал напряжением U_iср, т.е. формировать на каждом полупериоде любую нужную форму напряжения, как показано на рис. 4.22,б. С увеличением n будет уменьшаться t и ступенчатая кривая будет приближаться к заданной плавной.

Используя широтно-импульсную модуляцию, можно формировать любые нужные формы кривой тока, учитывая изменяющиеся в процессе работы параметры нагрузки. В современных хорошо сделанных преобразователях частоты ШИМ позволяет при любой требуемой выходной частоте преобразователя изменять нужным образом амплитуду напряжения, управляя магнитным потоком двигателя, и формировать при любой нагрузке на валу близкую к синусоидальной форму тока двигателя.

Полно реализовать широкие возможности ШИМ удалось лишь в последние 5 - 10 лет с появлением на рынке совершенных ключей, в частности, транзисторных модулей IGBT с напряжением до 1200 В, током до 600 А и частотой коммутации до 30 кГц, а также средств управления ими.

На рис. 4.23 в качестве примера показаны экспериментальные осциллограммы фазного напряжения и тока в одной из версий системы ПЧ-АД.

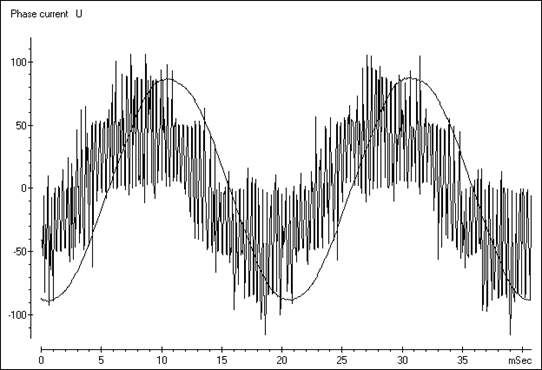
Рис. 4.23. Экспериментальная осциллограмма напряжения и тока в ПЧ с ШИМ

Наряду с рассмотренными выше преобразователями частоты с явно выраженным звеном постоянного тока иногда используются преобразователи частоты, в которых нет промежуточного звена постоянного тока, а питающая трехфазная сеть непосредственно связана с нагрузкой - статорными обмотками АД через группы управляемых выпрямителей - рис. 4.24,а,б. Такие ПЧ называют преобразователями частоты с непосредственной связью или циклоконверторами.

Каждая фаза двигателя (на рис. 4.24,б изображена фаза А) снабжена двумя комплектами встречно-параллельно включенных управляемых выпрямителей, выполненных на простейших полууправляемых ключах - тиристорах. Управляя выпрямителями, можно обеспечить условия, при которых на каждой фазе двигателя в положительный полупериод требуемого выходного напряжения (“+” на рис. 4.24,в) проводит один комплект тиристоров А1, а в отрицательный (“-”) другой - А2.

а) б)

в)

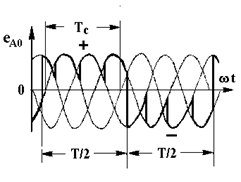
Рис. 4.24. Схемы (а) и (б) и диаграмма напряжений (в) преобразователя частоты с непосредственной связью

Из рис. 4.24,в следует, что период выходного напряжения Т и, следовательно, частота f= 1/Т зависят от момента переключения комплектов тиристоров и могут изменяться в некоторых пределах. Верхняя частота ограничена, поскольку при приближении Т к Т_с (периоду сетевого напряжения) выходное напряжение оказывается сильно искаженным; на практике часто принимают f £ f_c/2.

Амплитуда выходного напряжения может изменяться за счет изменения угла, как показано на рис. 4.24,в.

К преимуществам циклоконвертора следует отнести схемную простоту, реализуемость на простых, дешевых ключах, возможность двусторонней передачи мощности, малые потери в силовом канале. Однако, его недостатки - низкая верхняя частота, сильное искажение как питающего, так и выходного напряжения ограничивают пока его применение лишь отдельными специальными приводами.

Как следует из изложенного выше, преобразователи частоты являются одновременно и регуляторами напряжения, однако эта их функция имеет вспомогательный характер.

Вместе с тем, имеется специальная группа электрических преобразователей - регуляторы напряжения, единственной функцией которых является управление средней за полпериода величиной переменного напряжения.

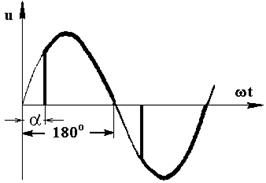
Типичная схема трехфазного тиристорного регулятора (преобразователя) напряжения ТПН, включаемого между сетью переменного тока и нагрузкой (АД), представлена на рис. 4.25,а.

Три пары встречно-параллельно включенных тиристоров управляются блоком управления БУ, представляющим собой любое устройство типа СИФУ (схема импульсно-фазового управления). СИФУ подает на тиристоры открывающие импульсы в моменты, сдвинутые на изменяемый угол a относительно момента естественной коммутации, благодаря чему напряжение меняется от U = U_н (a = 0) теоретически до 0 (a = 180°) (рис. 4.25,б). Закрывание тиристоров происходит естественно - при изменении полярности напряжения.

а) б)

Рис. 4.25. Тиристорный регулятор напряжения

Регуляторы напряжения, отличающиеся предельной простотой, доступностью элементной базы (тиристоры), малыми габаритами, высокой надежностью и низкой стоимостью, давно используются в мировой практике в качестве регуляторов скорости маломощных, обычно однофазных двигателей (доли кВт) и в качестве устройств плавного пуска трехфазных двигателей значительной (десятки - сотни кВт) мощности. Они же могут использоваться и для управления напряжением в целях энергосбережения при w» const, но сильно меняющейся нагрузке.

Как подчеркивалось ранее, эти устройства не должны применяться для регулирования скорости сколько-нибудь мощных АД, приводящих во вращение насосы, вентиляторы и другие машины, работающие в продолжительном режиме.

РАЗДЕЛ ПЯТЫЙ

ПЕРЕХОДНЫЕ ПРОЦЕССЫ

В предыдущих разделах изучались свойства и характеристики электроприводов в установившихся режимах, то есть при выполнении условия

М - М_с = 0.

В настоящей главе рассматриваются неустановившиеся или переходные процессы, имеющие место при переходе привода из одного установившегося состояния в другое, совершающемся во времени. При этом

Можно назвать следующие причины возникновения переходных процессов:

изменение М_с;

изменение М, то есть переход привода с одной характеристики на другую, имеющий место при пуске, торможении, реверсе, регулировании скорости, изменении какого-либо параметра привода.

Необходимость в анализе переходных процессов возникает в связи с тем, что производительность ряда ответственных механизмов (например, реверсивного прокатного стана) определяется быстротой протекания переходных процессов; качество выполнения многих технологических операций определяется переходными процессами (движение лифта, врезание резца в деталь и т.п.); механические и электрические перегрузки оборудования в большинстве случаев определяются переходными процессами.

Объектом исследования, как и прежде, будет упрощенная, идеализированная модель привода - рис. 5.1.

Рис. 5.1. Модель электропривода для исследования динамики

Основная задача при изучении переходных процессов сводится к определению зависимостей w(t), M(t) и i(t) для любых конкретных приводов в любых условиях.

При изучении переходных процессов мы будем полагать известными следующие исходные данные:

- начальное состояние: w_нач, М_нач, i_нач;

- конечное состояние: w_кон, М_кон, i_кон и соответствующая ему характеристика w(М);

- характер изменения во времени фактора, вызвавшего переходный процесс;

- параметры привода.

Все возникающие на практике задачи в целях их упорядоченного изучения разделим на четыре большие группы.

1. Преобладающей инерционностью в приводе является механическая инерционность (J); электрические инерционности (L) малы или не проявляются. Фактор, вызывающий переходный процесс, изменяется скачкообразно (мгновенно) то есть много быстрее, чем скорость.

Примеры задач, относящихся к этой группе: мгновенный наброс и сброс нагрузки, пуск, реверс, торможение, регулирование скорости асинхронных двигателей при питании от сети, если не учитывать индуктивности обмоток; то же для двигателей постоянного тока независимого возбуждения если Ф = const, а L_я = 0, то же для двигателей последовательного или смешанного возбуждения, если L_я = L_в =0.

2. Преобладающая инерционность - механическая (J); индуктивности электрических цепей малы или не проявляются. Фактор, вызывающий переходный процесс, изменяется не мгновенно, то есть темп его изменения соизмерим с темпом изменения скорости w (“медленное” изменение воздействующего фактора).

Примеры: переходные процессы в системах управляемый преобразователь - двигатель постоянного тока, преобразователь частоты - асинхронный двигатель, если L = 0.

3. Механическая и электрическая инерционность соизмеримы; фактор, вызывающий переходный процесс, изменяется мгновенно.

Примеры: переходные процессы в приводе постоянного тока при Ф = var; то же при Ф = const, но L_я ¹ 0, то же в системе источник тока - двигатель.

4. Учитываются несколько инерционностей, фактор, вызывающий переходный процесс, изменяется не мгновенно. Эти наиболее сложные задачи, относящиеся к замкнутым системам регулирования, мы рассмотрим очень кратко - они будут детально изучаться в других курсах.

5.2. Переходные процессы при L = 0 и “быстрых” изменениях воздействующего фактора

Все переходные процессы, относящиеся к первой группе, подчиняются, очевидно, механическому уравнению движения

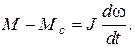(5.1)

Искомые зависимости w(t) и M(t) должны быть получены путем решения этого уравнения при заданных начальных условиях. Конкретные особенности привода отразятся в виде зависимостей M(w) и M_с(w), входящих в уравнение (5.1).

а) M = const, M_с = const

Начнем рассмотрение задач первой группы с простейшего случая, когда в переходном процессе M = const, и M_с = const.

а) б)

Рис. 5.2. Механические характеристики (а) и временные зависимости (б) при М = const и M_c = const

Пусть привод (рис. 5.1) работал в точке w _нач, М _нач = М _с (рис. 5.2) некоторой характеристики (она нас не интересует) и в момент времени t = 0 был мгновенном переведен на новую характеристику, показанную на рис. 5.2,а жирной линией.

Уравнение (5.1) в этом случае - дифференциальное уравнение с разделяющимися переменными и его решение имеет вид:

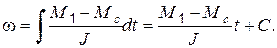
Постоянную интегрирования С найдем из начального условия - при t = 0, w = w _нач:

w _нач = С.

Окончательно будем иметь:

(5.2)

Это решение действует на интервале w _нач < w < w _кон, так как по условию при w = w _кон функция w(М) терпит излом. На этом интервале М =М₁.

Графики переходного процесса приведены на рис. 5.2,б. Время переходного процесса t _пп можно найти, подставив в (5.2) w = w _кон и решив относительно t:

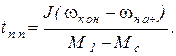(5.3)

Этот же результат, конечно, можно получить, решив (5.1) относительно dt и взяв определенный интеграл:

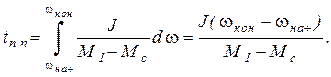
Рассмотренный простейший случай имеет очень большое практическое значение, так как к нему может быть сведено в целях оценки времени и характера переходного процесса большое число конкретных задач.

Пример. Оценить время пуска t_п и построить приближенный график переходного процесса пуска короткозамкнутого асинхронного двигателя с известными механической характеристикой, М_с и J (рис. 5.3,а). Заменим реальную характеристику (сплошная линия) приближенной (пунктирная линия) и применив (5.3), получим:

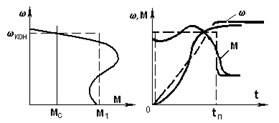
а) б)

Рис. 5.3. Механические характеристики (а) и графики переходных процессов

w(t) и M(t) при пуске асинхронного двигателя

.

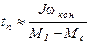Зная t_п, можно построить приближенные графики переходного процесса (пунктир на рис. 5.3,б). Эти графики будут отличаться от действительных (сплошные линии на рис. 5.3,б), однако во многих случаях полученная оценка может быть весьма полезной.

б) М_с = const, M линейно зависит от w, b < 0.

Пусть характеристики двигателя и механизма имеют вид, представленный на рис. 5.4. Уравнение линейной механической характеристики двигателя с отрицательной жесткостью может быть записано как

Рис. 5.4. Механические характеристики и графики переходных процессов w(t) и M(t) при линейной зависимости w(М)

(5.4)

или

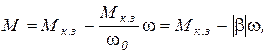(5.5)

где - жесткость механической характеристики; для линейной характеристики .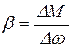

Подставив (5.5) в (5.1), после простых преобразований получим:

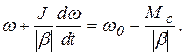
Выражение в правой части, как следует из (5.4), представляет собою w _кон. Обозначив коэффициент перед производной через Т _м, запишем:

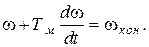(5.6)

Теперь подставим в (5.1) вместо 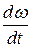ее выражение, полученное из (5.4):

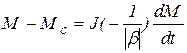
или, используя принятые выше обозначения,

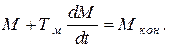(5.7)

Итак, мы обнаружили, что в рассматриваемом переходном процессе как для скорости, так и для момента справедливо одинаковое уравнение вида

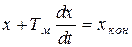, (5.8)

то есть линейное неоднородное дифференциальное уравнение с постоянной правой частью.

Коэффициент при производной

(5.9)

называют электромеханической постоянной времени.

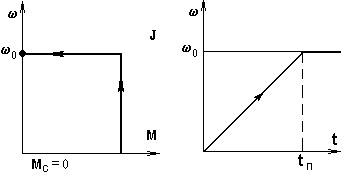
Рис. 5.5. К определению электромеханической постоянной времени Т_м

Для выяснения смысла этой величины рассмотрим условный привод с характеристикой, показанной на рис. 5.5. Определив время разгона такого привода по (5.3)

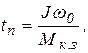
замечаем, что оно выражается так же, как Т _м. В связи с этим можно считать, что электромеханическая постоянная времени Т _м представляет собою время, за которое привод разогнался бы вхолостую до w = w₀ под действием момента короткого замыкания. Другие выражения для Т _м приведены в (5.9). В некоторых частных случаях оказывается удобным выражать Т _м через параметры привода. Так, для двигателя постоянного тока независимого возбуждения можно выразить жесткость характеристики как (см. п. 3.2)

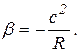
Подставив это выражение в (5.9), получим

(5.9,а)

Правая часть уравнения (5.8) представляет собою конечное значений переменной, то есть установившуюся величину, которая будет достигнута после окончания переходного процесса.

Решение (5.8), как известно, имеет вид

x = x_cв + х_пр = Ае^pt + х_кон,

где p - корень характеристического уравнения

1 + pТ_м = 0,

то есть

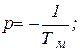
А - постоянная, определяемая из начального условия:

t = 0, x = x_нач,

то есть

А = х_нач - х_кон.

Итак, окончательно имеем:

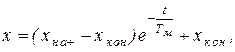(5.10)

то есть скорость и момент изменяются в переходном процессе от начальных до конечных значений по экспоненциальному закону с постоянной времени Т_м (см. рис. 5.4).

Напомним некоторые важные свойства экспоненты.

1. Касательная в любой точке отсекает на линии установившегося состояния отрезок, равный Т_м.

2. За время t = Т_м изменение величины составляет 0,632 от полного изменения.

3. За время t = 3 Т_м изменение составляет 0,95 от полного. В дальнейшем мы будем считать, что процесс устанавливается за t = 3 Т_м.

Уравнение (5.10) позволяет решать любые задачи, относящиеся к рассматриваемому типу.

Пример 1. Рассчитать переходный процесс мгновенного наброса нагрузки от М_с1 до М_с2 на асинхронный короткозамкнутый двигатель с механической характеристикой, линейной на рабочем участке (рис. 5.6).

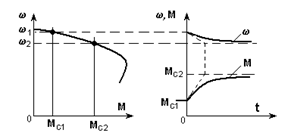
Рис.5.6. Переходный процесс наброса нагрузки

Вычислим Т_м:

Определим начальные и конечные значения w и М:

w_нач = w₁, w_кон = w₂;

М_нач = М_с1, М_кон = М_с2

Запишем по (5.10) уравнения переходного процесса

и построим графики (рис. 5.6).

Пример 2. Рассчитать переходный процесс пуска с одной ступенью пускового реостата и динамического торможения с самовозбуждением двигателя постоянного тока последовательного возбуждения; М_с - реактивный.

Построим сначала пусковую диаграмму и тормозную характеристику (рис. 5.7,а) - см. п.п. 3.2, 3.4. Если на рабочих участках характеристики близки к прямым, можно воспользоваться аналитическим решением задачи. В данном случае механические характеристики имеют разрывы (при w₃, w₁) и изломы (при w₄), поэтому необходимо разделить весь процесс на участки таким образом, чтобы в пределах каждого участка функции w(М) и w(М_с) были линейными и не имели изломов и разрывов.

а) б)

Рис. 5.7. Механические характеристики (а) и кривые переходных процессов (б) при реостатном пуске и динамическом торможении двигателя последовательного возбуждения

В нашем случае таких участков будет четыре:

I - 0< w < w₃ (пуск на реостатной характеристике);

II - w₃ < w < w₁ (пуск на естественной характеристике);

III - w₁ > w > w₄ (торможение с самовозбуждением);

IV - w₄ < w < 0 (торможение под действием М_с).

К первым трем участкам может быть применена формула (5.10), так как в пределах этих участков М(w) - линейные функции; к IV участку, где М = 0 и М_с = const, следует применить решение, полученное в п. а), т.е. формулу (5.2).

Обратим внимание на то, что отсчет времени в уравнениях (5.10) и (5.2), которыми мы будем пользоваться, ведется от момента t = 0, в который произошло изменение, вызвавшее переходный процесс. Поэтому, решая задачу по этапам, следует на каждом этапе отсчет времени вести от своего начала; общее время переходного процесса определится конечно, как сумма времени на этапах.

Для того, чтобы воспользоваться уравнениями (5.10) и (5.2), следует определить входящие в них начальные и конечные значения величин и постоянные времени.

Начальные значения скорости очевидны из графика w(М) - это фактические значения скорости в начале соответствующего этапа. При определении начальных значений момента следует помнить, что в рассматриваемых задачах мы пренебрегаем инерционностью электрических цепей и считаем, что ток, а следовательно, и момент изменяются мгновенно при изменении параметров привода, то есть при переходе с характеристики на характеристику. На графике w(М) это соответствует горизонтальным линиям - момент изменяется скачком при w = const. Поэтому в качестве начальных значений момента следует брать величины из графика w(М), получившиеся после соответствующего мгновенного изменения характеристики.

В качестве конечных значений w и М при использовании уравнения (5.10) следует всегда брать координаты точки пересечения двух прямых w(М) и w(М_с), то есть точки установившегося режима, независимо от того будет достигнут этот режим фактически или нет. Это важное правило вытекает из того, что уравнение (5.10) есть решение уравнения (5.8) именно при указанных условиях. Постоянные времени определяются для каждого этапа по (5.9).

Для рассматриваемой задачи начальные и конечные значения приведены в табл. 5.1 (следует обратить внимание на подчеркнутые величины).

Таблица 5.1

№№ этапов	wнач	wкон	Мнач	Мкон	Тм	Примечания
I		w2	М1	Мс		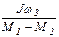Уравнение (5.10)
II	w3	w1	М1	Мс		Уравнение (5.10)
III	w1	- w5	-М3	Мс		Уравнение (5.10)
IV	w4				-	Уравнение (5.2) Процесс заканчивается при w =0, так как Мс - реактивный

Данные табл. 5.1 позволяют записать уравнения для каждого из четырех этапов и построить графики - рис. 5.7,б.

Пример 3. Рассчитать и построить кривые переходного процесса реверса двигателя постоянного тока независимого возбуждения, питающегося от сети U = const, при активном и реактивном характере М_с.

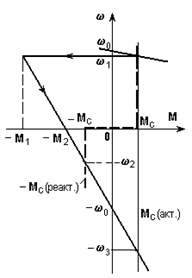
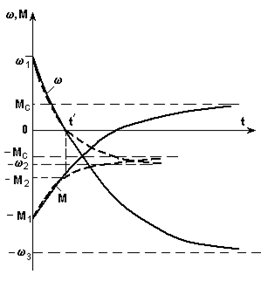
а) б)

Рис. 5.8. Механические характеристики (а) и кривые переходных процессов (б)

при реверсе электропривода

Решение, как всегда, начнем с построения графиков w(М) (рис. 5.8,а); график реактивного М_с построен жирными пунктирными линиями.

Рассмотрим сначала случай, когда М_с активный. При этом, очевидно, переходный процесс протекает в один этап, а его уравнения, полученные из (5.10), имеют вид:

где

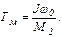
Соответствующие графики построены на рис. 5.8,б сплошными линиями.

При реактивном М_с, изменяющем знак при w = 0, необходимо рассматривать два этапа: I от w₁ до w = 0 и II от w = 0 до w = - w₂. На I этапе уравнения не будут отличаться от полученных ранее. Действительно, на этом этапе реактивный характер М_с не проявляется и он, как и в первом случае, способствует торможению привода. Этот результат соответствует правилу, изложенному в предыдущем примере.

На II этапе изменяется знак М_с и, в противоположность предыдущему случаю, М_с оказывает тормозящее действие при разгоне привода в противоположную сторону. Уравнения для этого этапа имеют вид:

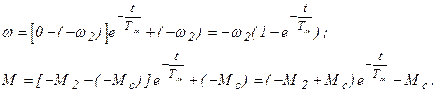
Графики переходных процессов при реактивном М_с построены на рис. 5.8,б пунктирными линиями. В момент времени t¢ кривые терпят излом, темп процесса замедляется, что связано со скачкообразным уменьшением динамического момента, обусловленным изменением знака М_с.

Если требуется найти зависимость i(t), следует воспользоваться известным соотношением

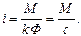
в) М_с = const, M - линейно зависит от w, b > 0

Рассмотренные выше переходные процессы при b < 0 соответствовали устойчивой точке установившегося режима w_кон, М_кон, то есть w и М, изменяясь, стремились к этой точке. Вместе с тем, иногда требуется рассчитывать переходные процессы при b > 0, что соответствует неустойчивой точке установившегося режима (см. п. 1.3) - рис. 5.9,а.

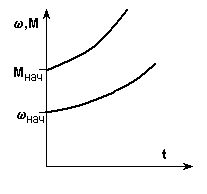
а) б)

Рис. 5.9. Механические характеристики (а) и кривые переходного

процесса (б) при b > 0

В этом случае уравнение механической характеристики привода запишется как

или

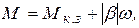
что приведет после подстановки этих выражений в (5.1) и выполнения преобразований к уравнению

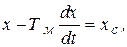(5.11)

где х - скорость или момент;

х_с - скорость или момент, соответствующие точке установившегося режима (см. рис. 5.9,а).

По сравнению с (5.8) в этом уравнении изменился знак перед производной, а в правой части стоит величина х_с, не имеющая теперь смысла конечного значения переменной.

Решим уравнение (5.11), как уравнение с разделяющимися переменными; кстати, мы могли бы решить этим приемом и уравнение (5.8):

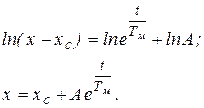
Использовав начальные условия t = 0, x = x_нач, получим

х = (х_нач - х_с) (5.12)

Графики w(t) и М(t), соответствующие (5.12), показаны на рис. 5.9,б.

г) М_с и М - линейные функции w.

Полученные в п.п. б) и в) результаты можно распространить на случай, когда М и М_с - линейные функции скорости.

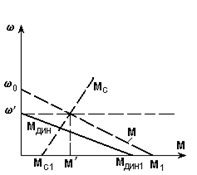
Рассмотрим эту возможность на простом примере. Пусть требуется рассчитать переходный процесс пуска привода, если характеристики двигателя и нагрузки заданы, как показано на рис. 5.10,а пунктиром.

а) б)

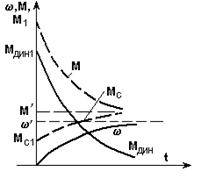
Рис. 5.10. Механические характеристики (а) и кривые переходных процессов (б)

при линейных зависимостях М(w) и М_с(w)

Заменим эти характеристики одной - зависимостью динамического момента М_дин = М - М_с от скорости. Эта зависимость линейна, так как линейны М(w) и М_с(w) - сплошная линия на рис. 5.10,а. Теперь, воспользовавшись полученными ранее результатами, можно получить зависимости w(t) и М_дин(t). При этом w _нач = 0, w _кон = w¢, М_{дин нач} = М_{дин 1}, М_{дин кон} = 0, ; кривые построены на рис. 5.10,б сплошными линиями. Если необходимо, можно построить и графики М(t) и М_с(t), так как известны начальные и конечные величины (рис. 5.10,а) и определена Т_м. Эти графики показаны на рис. 5.10,б пунктиром.

5.3. Переходные процессы при L=0 и “медленных” изменениях воздействующего фактора

К задачам данной группы ранее были отнесены переходные процессы в системе преобразователь - двигатель (П-Д). Фактор, вызывающий переходный процесс, изменяется не мгновенно (темп его изменения соизмерим с темпом изменения скорости привода в переходном процессе); учитывается только механическая инерция в приводе (J), индуктивности в цепях двигателя малы или не проявляются.

Типичные структуры системы П-Д и соответствующие механические характеристики показаны на рис. 5.11 и 5.12.

а) б)

Рис. 5.11. Система ПН-ДПТ и ее механические характеристики

Роль преобразователя П в схеме на рис. 5.11, как отмечалось, может играть генератор (система Г-Д) или тиристорный преобразователь (ТП-Д). Фактор, вызывающий переходный процесс в этих системах, - изменение входного сигнала u_вх, приводящее к изменению ЭДС преобразователя е_п.

а) б)

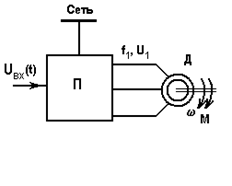
Рис. 5.12. Система ПЧ-АД и ее механические характеристики

Роль преобразователя П в схеме на рис. 5.12 играет статический преобразователь частоты. Фактор, вызывающий переходный процесс в этих системах, - изменение входного сигнала u_вх, приводящее к изменению частоты и напряжения на выходе преобразователя.

Как и прежде, целью изучения переходных процессов в системе П-Д будет определение зависимостей w(t), М(t) и иногда i(t) при известных условиях переходного процесса и параметрах привода.

Введем ряд условий и допущений.

1. Механические характеристики привода w(М) известны, линейны (по крайней мере, на рабочих участках) и параллельны друг другу, то есть выражаются уравнением (5.4):

где 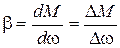- жесткость характеристик.

2. Известны или могут быть определены зависимости е_п(t) или f₁(t), то есть закон изменения во времени фактора, вызывающего переходный процесс. Так как е_п или f₁ однозначно связаны со скоростью идеального холостого хода привода w₀

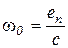- для схемы на рис. 5.11,

- для схемы на рис. 5.12,

то известен закон изменения во времени w₀.

3. Известно начальное (w_нач, М_нач) и конечное (w_кон, М_кон) состояние привода, момент инерции J и момент сопротивления М_с = const.

4. Преобразователь П обладает двусторонней проводимостью, то есть характеристики w(М) могут располагаться во всех квадрантах плоскости w, М.

Рассмотрим прежде всего качественные отличия переходных процессов в системе П-Д от изученных ранее случаев, когда е_п или f₁ изменялись мгновенно, то есть мгновенно устанавливалась соответствующая новая механическая характеристика, а изменение скорости w и момента М в переходном процессе происходило согласно именно этой характеристике. Переходный процесс определялся статической механической характеристикой привода.

В рассматриваемых далее задачах е_п или f₁ изменяются, как указывалось, не мгновенно, то есть переход привода с одной характеристики на другую происходит постепенно, одновременно с изменением скорости, в результате чего соответствие между скоростью w и моментом М в каждый момент времени определяется не статической механической характеристикой, а другой, отличной от нее характеристикой, которую мы далее будем называть динамической механической характеристикой или просто динамической характеристикой.

В качестве примера на рис. 5.13 показана статическая характеристика асинхронного двигателя при номинальной частоте 1, по которой будет происходить пуск при мгновенном приложении к двигателю напряжения такой частоты, и динамическая характеристика 2, соответствующая пуску двигателя путем плавного изменения частоты от нуля до номинальной по некоторому закону.

Рис. 5.13. Статическая 1 и динамическая 2 механические характеристики

Динамические характеристики определяются темпом изменения фактора, вызывающего переходный процесс, и параметрами привода, могут очень сильно отличаться от статических характеристик и даже иметь совсем другую форму.

Легко обнаружить связь зависимостей w(t) и М(t) с динамической характеристикой привода: исключив время t из уравнений w(t) и М(t), мы получим динамическую характеристику.

а) Уравнения, описывающие переходные процессы.

Из уравнения механической характеристики (5.4) получим:

М = ½ b ½ w₀ - ½ b ½ w. (5.5,а)

Подставив (5.5,а) в уравнение движения (5.1), после элементарных преобразований будем иметь:

(5.13)

Коэффициент при производной 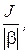как и раньше, - электромеханическая постоянная времени Т_м. Правая часть уравнения представляет собою скорость w_с, соответствующую моменту сопротивления М_с, однако, в рассматриваемом случае w₀, а значит и w_с не постоянные величины, а известные функции времени w₀(t) и w_c(t). Таким образом, уравнение (5.13) имеет вид:

. (5.14)

Решение этого дифференциального уравнения определит искомую зависимость w(t).

Для получения зависимости М(t) удобно воспользоваться непосредственно уравнением движения (5.1), подставив в него производную найденной функции w(t):

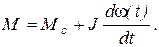(5.15)

Правая часть уравнения (5.14), вообще говоря, может иметь любой вид. Закон w₀(t) в случае безынерционного преобразователя формируется на его входе; при инерционном преобразователе закон w₀(t) связан со свойствами преобразователя. В ряде случаев закон w₀(t) формируется таким образом, чтобы получить требуемый закон w(t).

б) Уравнение переходных процессов при линейном законе w_с(t)

Получим решение уравнения (5.14) для одного важного вида функции w_с(t) - для линейного изменения w_с во времени:

w_с(t) = а + kt. (5.16)

Такой закон может быть сформирован при безынерционном преобразователе с помощью задатчика интенсивности.

Мы используем здесь общее уравнение прямой, не накладывая пока никаких ограничений на величины а и k с тем, чтобы, рассматривая частные случаи, можно было пользоваться полученным общим результатом.

Уравнение (5.14) с учетом (5.16) имеем вид:

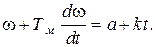(5.17)

Решение будем искать, как и прежде, в виде суммы свободной w_св и принужденной w_пр составляющих:

w = w_св + w_пр. (*)

Свободная составляющая, то есть решение однородного уравнения, полученного из (5.17) имеет вид:

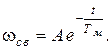
Принужденную составляющую будем искать, учитывая (5.16), в виде:

w_пр = В + kt,

так как в установившемся режиме скорость будет линейно изменяться во времени. Подставив w_пр в (5.17) получим:

В + kt + kT_м = a + kt

или

B = a - kT _м.

Подставим теперь w_св и w_пр в (*):

Постоянную А найдем, используя начальные условия: при t = 0 w = w_нач:

w_нач = А + а - kT_м,

откуда

А = w_нач - а + kT_м

Окончательно будем иметь:

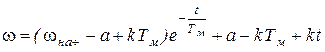. (5.18)

Перейдем теперь к рассмотрению некоторых конкретных переходных процессов в системе П-Д.

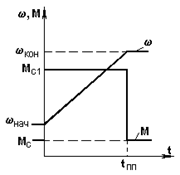
в) Пуск вхолостую.

Будем полагать, что закон изменения во времени фактора, вызывающего переходный процесс, е_п или f₁ или в общем случае w₀ имеет вид, представленный на рис. 5.14 справа вверху. Так как М_с = 0 (пуск вхолостую), то w_с = (t) будет совпадать с w₀(t) - см. уравнение (5.13), т.е. а = 0 и

где e - ускорение, характеризующее темп изменения w₀;

при 0 < t < t₁ w_с(t) = et;

при t > t₁ w_с(t) = w₀₁ = сonst.

Излом функции w_с(t) при t = t₁ свидетельствует о том что переходный процесс состоит из двух этапов, и его необходимо рассчитать отдельно для каждого участка.

I этап (0 < t < t₁).

Приняв, что при t = 0 w_нач = 0 и подставив в (5.18) а = 0, k = e, получим

(5.19)

Рис. 5.14. Механические характеристики и графики переходного процесса при пуске вхолостую с w₀(t) = et

Воспользовавшись уравнением (5.15), найдем закон изменения момента во времени:

(5.20)

Проанализируем полученные уравнения.

Ускорение привода определится как

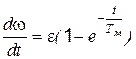
и при t = 0 Этот результат очевиден: при t = 0 w_с = w₀ = 0 т.е. е_п = 0 или f₁ = 0, привод не развивает момента и в соответствии с уравнением движения (5.1) и .

При t > 3Т_м 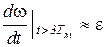, т.е. скорость изменяется в том же темпе, что и фактор, вызывающий переходный процесс. Из уравнения (5.19) следует, что при t > 3Т_м

w = e (t - Т_м) = w_с(t) - e Т_{м .} (5.19,а)

Графики w_с(t) и w(t) представлены на рис. 5.14. Кривая w(t) сдвинута вправо относительно кривой w_с(t) на величину Т_м; в каждый момент времени при t > 3Т_м разница между w_с и w составляет e Т_м.

Момент в соответствии с (5.20) возрастает по экспоненциальному закону (см. рис. 5.14) и при t > 3Т_м достигает величины

M_макс = J e. (5.20,а)

Это соотношение позволяет оценить допустимую величину e. Действительно, если считать, что в переходном процессе М_макс = М_доп, то

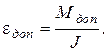
В частности, можно найти минимальное время пуска привода при котором момент не превысит допустимого значения:

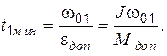
Если положить, что М_доп = 2 М_н, а , что справедливо для нормальной электрической машины средней мощности, то получим

II этап (t > t₁).

На II этапе w_с = w₀₁, а значит, и е_п или f₁ имеют постоянную величину. Переходный процесс в этом случае ничем не отличается от рассмотренных ранее переходных процессов, отнесенных к первой группе задач. Если отсчитывать время от t₁, (точка 0’), то скорость w и момент М будут изменяться в соответствии с уравнением (5.10); в качестве х_нач следует принять значения w и М в момент времени t₁. Если t₁< 3Т_м, начальные значения должны быть лпределены по (5.19) и (5.20) при подстановке в эти уравнения t = t₁.

В качестве х_кон, очевидно, следует взять w₀₁ и 0.

Графики w(t) и M(t) на II этапе показаны на рис. 5.14. Там же слева приведена динамическая механическая характеристка для случая пуска вхолостую.

Все рассмотренные выше величины и зависимости имеют очевидный физический смысл для системы П-Д с двигателем постоянного тока. Действительно,

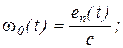
т.е. кривая w₀(t) представляет собою в некотором масштабе закон изменения во времени е_п, а кривая w(t) - закон изменения е в том же масштабе. Разность этих величин в соответствии с вторым законом Кирхгофа определит ток, протекающий в якорной цепи:

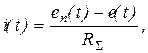
а значит, и момент, развиваемый двигателем

M(t) = ci(t).

г) Реверс (торможение) вхолостую.

Для осуществления реверса w₀ должна изменить направление. Это значит, что е_п уменьшается до 0, затем изменяет полярность и возрастает до заданной величины, либо f₁ уменьшается до 0, меняется чередование фаз и f₁ возрастает до заданной величины.

Как и прежде, будем считать, что изменение w₀ во времени осуществляется по линейному закону при (0 < t < t₁), затем при t > t₁ w₀ = w₀₁. Таким образом, переходный процесс состоит из двух участков, которые следует рассматривать отдельно. Так как переходный процесс осуществляется вхолостую (М_с = 0), то w_с(t) = w₀(t).

I этап (0 < t < t₁).

На I этапе изменение w_с(t) можно представить уравнением (5.16), подставив в него а = w₀₁, k = -e. Тогда, воспользовавшись уравнением (5.18), в котором w_нач = w₀₁, получим

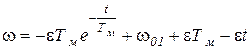
или

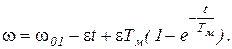(5.21)

Уравнение (5.16) определяет закон изменения М во времени:

(5.22)

Проанализируем полученные уравнения.

Ускорение привода

При t = 0 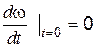, что очевидно и с физической точки зрения: при t = 0 М = 0 т.е. и .

При t > 3Т_м , т.е. как и при пуске, скорость изменяется в том же темпе, что и фактор, вызвавший переходный процесс. При t > 3Т_м

w = w₀₁ - e (t - Т_м) = w_с(t) + e Т_{м ,}

т.е. как и при пуске, кривая w(t) располагается правее кривой w_с(t), причем сдвиг по оси t составляет величину Т_м, а в каждый момент времени при t > 3Т_м разница между w_с и w составляет e Т_м.

Момент отрицателен и изменяется по экспоненциальному закону до величины

M_макс = - J e.

II этап (t > t₁).

Переходные процессы на II этапе подчиняются уравнению (5.10) и рассчитывается очевидным образом.

Кривые w_с(t), w(t) и М(t) и динамическая характеристика показаны на рис. 5.15.

Рис. 5.15. Механические характеристики и графики переходного

процесса при реверсе вхолостую с w₀(t) = -et

При торможении вхолостую w₀ изменяется от значения w₀₁ до нуля. Как и при реверсе, процесс состоит из двух этапов, причем на I этапе (0 < t < t₁) кривые w(t) и М(t) не отличаются от аналогичных кривых при реверсе, а на II этапе - подчиняются уравнению (5.10) с соответствующими х_нач и х_кон.

Кривые w(t) и М(t), а также динамическая характеристика показана на рис. 5.16.

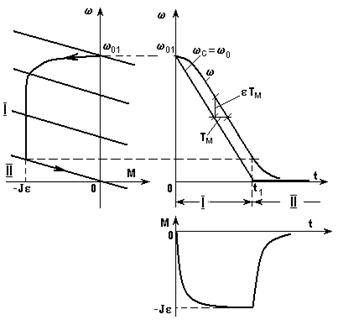
Рис. 5.16. Механические характеристики и графики переходного

процесса при торможении вхолостую с w₀(t) = -et

Рассмотрим кратко порядок операций при построении кривых переходного процесса в рассматриваемых случаях.

1. Изображается w_с(t), в рассмотренных случаях w_с(t) = w₀(t); отмечаются этапы и определяется e на этапе, где w_с(t) изменяется.

2. Проводится линия, параллельная w_с(t) и сдвинутая вправо на Т_м, - это и будет основа графика w(t).

3. Корректируется график w(t) на начальном и конечном (II) участках, введением экспонент с постоянной времени Т_м.

4. Строится основа графика М(t) - прямоугольник со сторонами 0 - t₁ и J e; в случае реверса и торможения e имеет отрицательный знак.<

Дата добавления: 2014-01-05