Переходные процессы в системах

Рассмотренные ранее случаи переходных процессов относятся к простейшим электроприводам, когда учитываются лишь основные накопители энергии и можно уделять внимание физической стороне дела, относительно просто приходя к результату. Вместе с тем, все современные электроприводы представляют собой весьма сложные многоэлементные замкнутые системы, и для их анализа и синтеза приходится прибегать к приемам, разработанным в теории автоматического управления. Один из самых распространеных на практике приемов - использование структурных схем с передаточными функциями входящих в систему элементов.

Передаточная функция - отношение изображений по Лапласу выходной величины к входной при нулевых начальных условиях. Так, для цепи R - L, подключенной к источнику напряжения u(t) имеем:

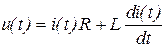
или, заменив 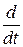на р, u(t) на u(p) и i(t) на i(p) и решив уравнение относительно i(p), принятом за выходную величину, получим

где - постоянная времени.

Для двигателя постоянного тока независимого возбуждения с учетом индуктивности якорной цепи L_я при питании якоря от источника напряжения u(t) и kФ = с, приняв за выходную величину w(t) и за входную u(t) после перехода к изображениям, получим для случая М_с = 0 структурную схему на рис. 5.25,а.

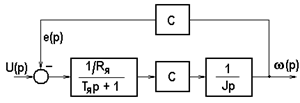
а)

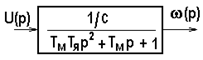
б) в)

Рис.5.25. Передаточные функции двигателя постоянного тока

независимого возбуждения

Проделав элементарные преобразования, будем иметь передаточную функцию двигателя в виде колебательного звена (рис. 5.25,б):

,

где - электромеханическая постоянная времени,

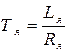- постоянная времени цепи якоря.

Если корни характеристического уравнения действительные, будем иметь два апериодических звена (рис. 5.25, в):

.

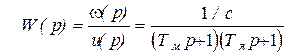Используя подобные действия, можно получить структурную схему любой системы и применить к ней приемы преобразования. анализа и синтеза, разработанные в теории автоматического регулирования.

Рассмотрим здесь кратко лишь один из таких приемов рационального управления динамической системой - построение систем подчиненного регулирования с последовательной коррекцией.

Для выходной координаты некоторого объекта регулирования образуют замкнутый контур, в который входит как сам объект, так и специальный регулятор, обеспечивающий заданное качество регулирования.

Пусть передаточная функция объекта регулирования имеет вид, к которому часто удается привести после преобразований передаточную функцию реального устройства:

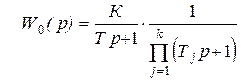, (5.31)

где К - общий коэффициент передачи,

Т - наибольшая постоянная времени,

Т_j - малые постоянные времени.

Поставим задачу максимально сократить время переходного процесса, исключив колебательность.

Рассмотрим сначала первый сомножитель в (5.31).

Теоретически возможно увеличить коэффициент передачи, включив на вход регулятор с передаточной функцией W_p(р)= K₁, однако это повысит чувствительность к помехам и склонность к колебательности. Теоретически возможен регулятор с передаточной функцией W_p(р)= Tр+ 1, однако такой регулятор нереализуем физически. На практике обычно используют пропорционально-интегральный регулятор (ПИ-регулятор) с передаточной функцией

(5.32)

Тогда в разомкнутой структуре с таким регулятором будем иметь без второго сомножителя в (5.31):

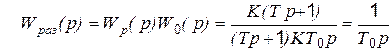. (5.33)

Для выбора Т₀ пользуются вторым сомножителем в (5.31). Если принять

(5.34)

то, как показано в теории, можно считать, что

(5.35)

Тогда, очевидно, передаточная функция разомкнутой системы будет

(5.36)

а передаточная функция замкнутой системы определится как

, (5.37)

где 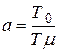- параметр, характеризующий вид переходного процесса; на рис. 5.26 приведены переходные функции для различных а. Очевидно, что компромисс между колебательностью и длительностью переходного процесса достигается при а = 2, и такая настройка (выбор Т₀) называется настройкой на технический оптимум. При этом без большой погрешности можно принять, что

(5.38)

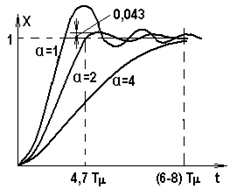
Рис. 5.26. Характер переходных процессов в контуре при

различных а = Т₀/Т_m

Итак, оптимизация объекта с передаточной функцией W₀(р) имеет компромиссный характер, осуществляется включением ПИ-регулятора W_р(р) с замыканием системы по выходной координате и состоит в замене разомкнутой структуры с большой постоянной времени Т замкнутой структурой с аналогичной передаточной функцией, но с другой постоянной времени, выбираемой из условия желаемого качества переходных процессов.

Изложенная процедура оптимизации особенно удобна и эффективна, если в систему входит несколько контуров - рис. 5.27. Начав с внутреннего (контур 1) и оптимизировав его, как было описано выше, переходят к следующему контуру (контур 2) и действуют аналогичным образом.

Рис. 5.27. Многоконтурная система

Если принять для упрощения, что малые постоянные Т_j, образовавшие некомпенсируемую постоянную Т_m, сосредоточены во внутреннем контуре, а во внешнем отсутствуют, можно получить следующие передаточные функции i -ого контура:

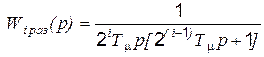(5.39)

и

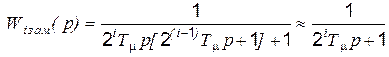. (5.40)

К достоинствам изложенной оптимизации относится идентичность переходных процессов в каждом контуре при их независимой настройке, простота ограничения координат за счет ограничения задания нелинейной характеристикой вход-выход соответствующего регулятора, удобство в практической наладке систем. К недостаткам можно отнести сравнительно низкое быстродействие внешних контуров - см. (5.40).

Приведенный пример оптимизации сложной системы, разумеется, далеко не исчерпывает всех возможностей. Так, в настоящее время с появлением эффективной компьютерной поддержки все чаще используется прием, состоящий в составлении поэлементного математического описания системы, представлении дифференциальных уравнений в форме Коши и использовании мощных пакетов типа Simnon, Simulink и др. для работы с полученным математическим описанием. Самым сложным, требующим немалых усилий здесь является этап получения адекватного математического описания. Остальное берет на себя мощный, хорошо организованный программный продукт.

РАЗДЕЛ ШЕСТОЙ

ЭНЕРГЕТИКА ЭЛЕКТРОПРИВОДА

Дата добавления: 2014-01-05