Інтерполяція

ЛЕКЦІЯ 2

ЦІЛЬ ЛЕКЦІЇ · викласти основні положення інтерполяції; · показати різницю між апроксимацією і інтерполяцією; · навести функції інтерполяції в програмному комплексі MathCAD; · дати приклад інтерполяції Ключові слова: інтерполяція, інтерполяційний многочлен, екстраполяція, інтерполяційні функції MathCAD  

У задачах теорії споруд постійно стикаємося з необхідністю обчислення значень функції заданою таблицею в точках, не співпадаючих з фіксованими в таблиці. Типовим прикладом є обчислення ординат лінії впливу в тих точках де прикладаються зосереджені сили. Ця рутинна нудна операція може бути повністю автоматизована, якщо удатися до інтерполяції.

¨	Визначення. Інтерполяція є наближене представлення функції заданою таблицею. Кінцевою метою інтерполяції є обчислення значень функції в точках, які не співпадають з фіксованими в таблиці.

З приведеного визначення, очевидно, що задача інтерполяції співпадає із задачею апроксимації. Загалом це так, але у пошуках функції інтерполяції потрібно додатково задовольнити важливій умові: шукана функція має єдиним чином проходити через точки інтерполяції.

Геометрично, задача інтерполяції для функції однієї змінної 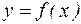означає побудову кривої, що проходить через задані точки (рис.1.3). Зверніть увагу, що поки задачі інтерполяції і апроксимації абсолютно ідентичні. Проте вже з рисунка інтуїтивно ясно, що через задані точки можна провести незліченну безліч різних кривих. Таким чином, задача відшукання функції f(x) по кінцевому числу її значень стає невизначеною.

—— f(x) _ _ _   Рис.1.3. Функції інтерполяції

Ця задача стає однозначною, якщо для функція інтерполяції f(x) заданої своїми n +1 значеннями вибрати многочлен 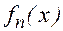ступеня не вище n, такий, що

, (1.6)

де 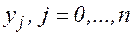- задані n +1 значень функції.

Многочлен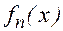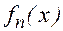задовольняючий цим умовам, називається інтерполяційним многочленом. Зверніть увагу, що сплайн, за визначенням, задовольняє умовам (1.6).

Якщо аргумент інтерполяції х знаходиться за межами відрізка інтерполяції, то задача визначення значень функції в довільних точках відрізка називається екстраполюванням

Дата добавления: 2014-01-05