Приклад 1.2

Приклад інтерполяції

Сплайнова інтерполяція

Лінійна інтерполяція

Функції інтерполяції програмного комплексу MathCAD

У програмному комплексі MathCAD є стандартні функції лінійної і сплайнової інтерполяції.

Функція, що обчислює за лінійною інтерполяцією для довільного аргументу х значення функції F(x), заданої своїми значеннями у фіксованих вузлах, має вид:

linterp(vx, vy, x),

де vx - вектор координат вузлів;

vy - вектор значень функції у вузлах;

x - координата для якої потребується обчислити значення функції.

Стандартна функція програмного комплексу MathCAD, яка обчислює в довільних точках інтерполяції за сплайном значення функції F(x),, заданої у фіксованих вузлах, має вид:

interр(S, vx, vy, x),

де vx - вектор координат вузлів;

vy - вектор значень функції в узлах;

x - координата для якої потребується обчислити значення функции.

S = cspline(vx, vy) – обчислює коефіцієнти сплайна;

Розглядається бездіфрагмова прогонова будова з прольотом 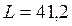м. У перерізі прогонової будови 9 балок. Ширина полиці балки 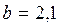м. Для крайньої балки, досить точним дискретним методом, у середньому перерізі, отримано 9 ординат лінії впливу тиску:

Lv ^T = [ 0.367 0.233 0.148 0.094 0.060 0.039 0.026 0.019 0.016 ]. Крок ординат є x_b=b=2,1 м.

Потрібно побудувати сплайнову функцію, що інтерполює лінію впливу тиску і знайти коефіцієнти поперечного розподілу двох колон навантаження А11 для =1,85м, де х₁ - відстань від початку координат до лівого крайнього вантажу навантаження А11 (рис. 1.4). Три інших координати отримуються за загальними правилами розміщення в поперечному перерізі прогонової будови навантаження А11:

x₂ = x₁ + 1,9 = 3,75 м; х₃ = х₂ + 1,1 = 4,85 м;

х₄ = х₃ + 1,9 = 6,75 м

Рис.1.4. Схема розміщення навантаження на прогоновій будові

На рис. 1.5 показано визначення сплайнового інтерполяційного поліному P(x) в системі MathCAD.

Коли інтерполяційний поліном визначено, процедура вирахування ординат в заданих точках стає зовсім простою – достатньо підставити задані координати в отриману функцію P(x) ( На рис. 1.5. функція позначена Ps(x)).

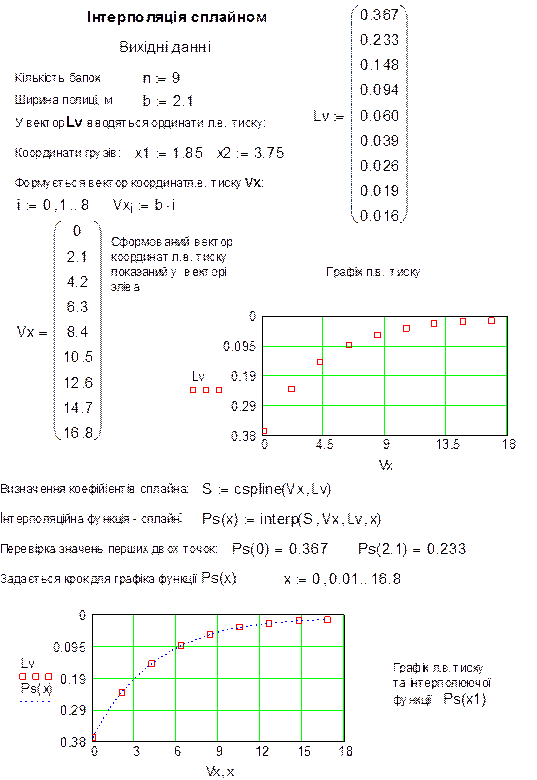
Рис. 1.6 Інтерполяція сплайном функції заданої таблицею

На рис. 1.7. показано обчислення коефіцієнту поперечного розподілу шляхом застосування отриманої вище функції інтерполяції ординат лінії впливу тиску на балку

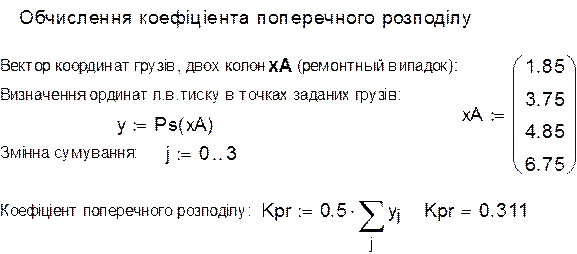
Рис. 1.7 Обчислення КПР за сплайновою інтерполяцією лінії впливу тиску

Дата добавления: 2014-01-05