Оценка генеральной дисперсии по исправленной выборочной дисперсии

Пусть из генеральной совокупностив резуль­тате n независимых наблюдений над количественным при­знаком X извлечена повторная выборка объема n:

При этом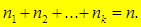

Требуется, по данным выборки, оценить (приближенно найти) неизвестную генеральную дисперсию D_Г. Если в ка­честве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематиче­ским ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что, как можно дока­зать, выборочная дисперсия является смещенной оценкой D_Г, другими словами, математическое ожидание выбороч­ной дисперсии не равно оцениваемой генеральной дисперсии, а равно:

(3.13)

Легко «исправить» выборочную дисперсиютак, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить D_В на дробь п/(п—1). Сделав это, получимисправленную дисперсию, которую обычно обозначают через s²:

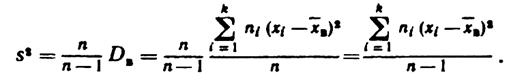
Исправленная дисперсия является, конечно, несме­щенной оценкой генеральной дисперсии. Действительно,

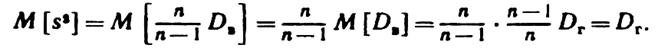
Итак,в качестве оценки генеральной дисперсиипри­нимаютисправленную дисперсию

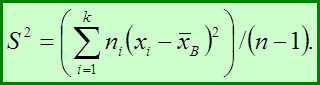(3.14)

Для оценки же среднего квадратического отклонения генеральной совокупности используют«исправленное» среднее квадратическое отклонение, которое равно квад­ратному корню из исправленной дисперсии:

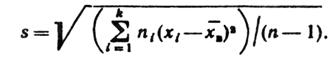(3.15)

Замечание. Сравнивая формулы

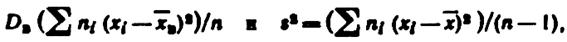
видим, чтоони отличаются лишь знаменателями. Очевидно, при достаточно больших значениях n объема выборкивыборочная и исправ­ленная дисперсииразличаются мало. На практикепользуются исправ­ленной дисперсией, еслипримерно n < 30.

4. Интервальные оценки неизвестных параметров распределения.

Дата добавления: 2014-01-05