Методика изучения геометрического материала

Задачи:

1. Сформировать представления о геометрических фигурах: точке, прямой, луче, отрезке, ломаной линии, угле, треугольнике, прямоугольнике, квадрате, многоугольнике и др..

2. Выработать практические умения построения геометрических фигур с помощью чертёжных инструментов.

Особенности изучения:

1. Не выделяется в отдельный раздел.

2. Элементы геометрии непосредственно связаны с изучением арифметического и алгебраического материала.

3. Преобладающие методы – наглядно-иллюстративный и практический.

4. Широко используются приёмы сравнения, варьирования несуществующих признаков.

Порядок изучения: (см. программы и учебники разных авторов).

Особенности изучения различных геометрических понятий:

При изучении чисел в концентре «Десяток» учащиеся используют геометрический материал как счётный, но, наряду с этим, идёт формирование представлений о геометрических фигурах, учитель ставит цель – показать детям, что форма фигуры не зависит от цвета, расположения и размера. Она зависит от числа элементов – количества углов и сторон. Упражнения:

§ На доске прикреплены фигуры разной формы, размера, цвета и материала. Учитель просит детей отобрать треугольники и проверить свой выбор пересчетом сторон и углов. Отобрать четырёхугольники, круги.

§ Из полосок различной длины, из спичек сконструировать модели различных геометрических фигур.

§ Изобразить треугольник, четырёхугольник, квадрат, круг.

Знакомство с отрезком происходит довольно рано, ещё в первом классе. Для введения понятия отрезка учитель использует метод демонстрации. Он вызывает двух учеников и предлагает им натянуть в руках нитку или верёвку. Показывает концы нити и формулирует первое определение. Расстояние между концами нити – это отрезок. Затем учитель показывает палочки разной длины, стороны знакомых геометрических фигур и сообщает, что это тоже отрезки. Потом учитель просит детей привести примеры отрезков, которые можно увидеть в классной комнате.

Следующий этап – это изображение отрезков на доске и в тетради. Учитель говорит, что чертить отрезок надо по линейке, т.к. край линейки – это тоже отрезок. Концы отрезка обозначаются чёрточками. Для того чтобы начертить отрезок заданной длины, надо:

1. Поставить точку – начало отрезка.

2. Совместить нулевую отметку на линейке с началом отрезка.

3. Провести по линейке прямую линию.

4. Закончить линию на отметке, соответствующей заданной длине отрезка.

5. Обозначить концы отрезка чёрточками.

Затем показывается, как измерить длину отрезка. В дальнейшем, длина отрезка используется для нахождения длины ломаной линии и суммы длин сторон прямоугольника и треугольника.

При формировании представлений об углах используется метод демонстрации в сочетании с практической работой.

Сначала учитель показывает получение прямого угла путём перегибания листа бумаги. Устанавливается, что две пересекающиеся линии сгиба делят лист бумаги на 4 части, на 4 угла. Путём перегибания и наложения учитель показывает, что все четыре угла равны и называются прямыми углами.

С помощью модели прямого угла учащиеся отыскивают прямые и непрямые углы на окружающих предметах. Для этого надо:

1. Совместить модель прямого угла с вершиной измеряемого угла и одну из сторон модели с соответствующей стороной данного угла.

2. Если вторая сторона модели будет проходить внутри измеряемого угла, то измеряемый угол больше прямого угла, такой угол называется тупым.

3. Если вторая сторона модели будет проходить вне измеряемого угла, то измеряемый угол меньше прямого угла, такой угол называется острым.

4. Если стороны и вершины модели и измеряемого угла совпадают, то измеряемый угол – прямой.

Так же необходимо показать, что угол – это часть плоскости. Контур угла делит плоскость на внутреннюю и внешнюю область угла.

По программе Моро измерение углов связано только со сравнением их с моделью прямого угла. По программе Петерсон детей знакомят с понятием градуса и градусной меры угла и учат измерять градусную меру угла с помощью транспортира. При этом решаются задачи:

§ Начертить угол заданной градусной меры.

§ Найти градусную меру угла.

Вводится буквенное обозначение углов, и решаются задачи вычислительного характера с градусными мерами углов. Например:

§ «Угол АВС равен 30 градусам, угол СВД – 40 градусам. Найдите градусную меру угла АВД.

§ Угол АВД состоит из углов АВС и СВД. Угол АВС равен 30 градусам, угол АВД – 70 градусам. Найдите градусную меру угла СВД» и др.

Знакомство с понятием прямоугольника можно провести на наглядной основе, используя метод демонстрации. На доске изображены различные четырёхугольники и перед детьми ставится задача определить количество прямых углов в каждом из них. Дети выполняют эту работу с помощью модели прямого угла. Находят четырёхугольники, у которых все углы прямые. Делается вывод: четырёхугольники, у которых все углы прямые, называются прямоугольниками.

Для закрепления детям предлагается найти прямоугольники в окружающей среде, и чертят прямоугольник в тетради.

Кроме понятия прямоугольника, учащиеся знакомятся со свойствами противолежащих сторон прямоугольника. Здесь необходимо:

1. Выделить понятие противолежащих сторон, используя для этого иллюстрации в учебнике.

2. На основе практической работы (измерением по линейке и наложением) подвести к выводу, что противолежащие стороны прямоугольника равны.

В дальнейшем, это свойство используется для вывода формулы периметра прямоугольника.

При знакомстве с понятием квадрата учитель прикрепляет к доске различные прямоугольники и предлагает детям найти длины сторон этих фигур, затем отобрать те, у которых все стороны равны. Сообщает, что прямоугольники, у которых все стороны равны, называются квадратам. Важно обратить внимание учащихся на то, что все квадраты – это прямоугольники, но не все прямоугольники - квадраты. Затем учащиеся находят предметы квадратной формы в окружающей среде и чертят квадраты с помощью линейки на линованной бумаге. Отдельные уроки посвящены выводу формул периметра прямоугольника и квадрата, а так же площадей этих фигур. Через площадь прямоугольника выводится площадь прямоугольного треугольника (основано на особенности: диагональ делит прямоугольник на два прямоугольных равных треугольника).

По программам, отличным от Моро, кроме обозначенных понятий детей знакомят с понятиями: ломаной линии, замкнутой и незамкнутой, длиной ломаной линии (в дальнейшем это понятие связывают с понятием многоугольника), окружности и куга, радиуса и диаметра окружности, симметрия осевая и центральная, пространственные тела: призма, прямоугольный параллелепипед, куб, пирамида, цилиндр, конус, шар, сфера. В основном эти понятия вводятся на уровне распознавания графических изображений.

На основе изученного геометрического материала решают задачи трёх видов:

1. Геометрические величины, как одни из рассматриваемых величин. Например: «Найдите площадь двухкомнатной квартиры, если площадь гостиной 12м², площадь спальни на 3м² меньше площади гостиной, площадь кухни в 2 раза меньше площади гостиной, а площадь коридора, туалета и ванной комната, вместе взятых, составляет 2\3 площади гостиной ».

2. Задачи на вычисление площадей, периметров и длин сторон. Например: «Периметр прямоугольника равен 12 см. Найдите его площадь, если одна из его сторон равна 4 см».

3. «Особые» задачи:

· задачи на распознавание.

· задачи на конструирование.

· задачи деления фигур на части.

Обобщению представлений о многоугольниках способствуют задачи на распознавание. Эти задачи представлены в виде следующих упражнений:

1 класс – На доске расположены модели геометрических фигур. Выберите из данных фигур треугольники.

Закрась на рисунке четырёхугольники - синим цветом, а треугольники красным.

Раздели все фигуры на две группы.

Учитель загадывает фигуру: я взяла красную фигуру, имеющую 4 угла, какую фигуру я взяла?

Сначала детям предлагаются для рассмотрения отдельные фигуры, затем комбинации фигур, причём цвет выступает помощником. Например,найдите 5 квадратов на рисунке.

2 класс – Из большой фигуры вычленить определённое число конкретных фигур. Например, найдите на чертеже 8 треугольников. 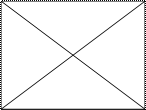Причём, цвет не является помощником или отсутствует совсем. Затем задание усложняется: покажите на чертеже все треугольники, сколько их? И, наконец, какие геометрические фигуры вы видите на чертеже? Сколько их? Покажите их на чертеже.

После того, как дети научатся обозначать фигуры латинскими буквами, задание усложняется: назови все треугольники – АВС, ВСД,…

Или, назовите треугольники, которым 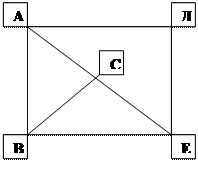принадлежит точка М.

Задачи на конструирование рассматриваются уже в 1 классе. Здесь они выполняются по образцу. Причём образец и количество объектов для конструирования одинаково.

Например, сложи из трёх спичек (счётных палочек) треугольник, из 4 спичек (счётных палочек) - квадрат.

Составьте из двух треугольников квадрат по образцу.

Затем, количество объектов для конструирования становится больше, чем элементов образца, а потом отсутствует и образец. К работе даётся словесный комментарий. Например, составьте из квадрата и двух треугольников прямоугольник, трапецию, параллелограмм. Интересны и творческие задания. Например, составьте из данных геометрических фигур изображение собаки, жираф, домика и т. д.

Задачи деления фигуры на части связано с двумя темами в математике:

§ Изучение площади – разбить квадрат на два равных треугольника, на прямоугольник и два треугольника.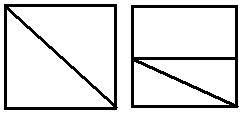

§ Понятие доли – разбейте квадрат на 4 равные части и закрасьте одну из них.

§ Понятие дроби – разбейте прямоугольник на 8 равных частей и закрасьте 3 из них.

Дата добавления: 2014-01-05