Методика изучения долей и дробей

Задачи:

1. Научить образовывать доли и дроби.

2. Научить называть и записывать доли и дроби (запись их предусмотрена не во всех программах).

3. Сравнивать доли и дроби.

4. Решать задачи на доли и дроби.

Этот материал изучается в 3-4 классах. Создаётся конкретное представление о доле и дроби на практической основе с использованием дидактического материала. Эта тема служит предварительной основой для изучения в 5-6 классах.

Источники получения долей и дробей:

1. Деление предметов на равные части.

2. Измерение величин.

3. Действия над числами (деление).

В начальной школе доли и дроби получают только на основании деления предмета на равные части, т. к. дети должны получить конкретное представление об этих понятиях.

Конкретное представление о долях создаётся в результате выполнения практической работы с демонстрацией. Учитель делит яблоко на две равные части и говорит, что каждая из равных частей называется половиной и ещё 1\2, показывает, что таких половин две в целом яблоке. Затем учитель делит яблоко на четыре равные части, каждая часть называется – четверть или 1\4 и таких четвёртых долей в целом яблоке четыре. Потом сообщается, что для записи долей необходимо два числа и черта (m\n). Причём, число, стоящее под чертой (дробная черта), показывает, на сколько равных частей разделили целое (знаменатель), а число, стоящее над чертой – сколько таких равных частей взяли (числитель).

Закрепление:

§ Практическая работа: детям выдаются полоски бумаги, и предлагается разделить их перегибанием на 2 равные части, на 4, на 8, сказать, как называется каждая часть, закрасить 1\2, 1\4, 1\8 отрезка.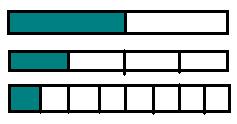

§ Рассматриваются рисунки с геометрическими фигурами, разбитыми на равные части подписанным названием частей. Дети должны объяснить смысл записи.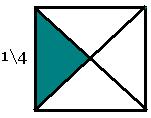

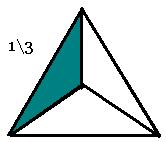
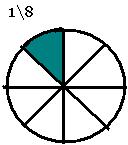
§ Предлагается начертить квадрат с заданной длиной стороны, разбить его на 2, 3, 4. 6, 8 равных частей, закрасить одну из них, назвать, записать. Возможны различные варианты разбиения, но должно учитываться одно условие – все части одинаковые.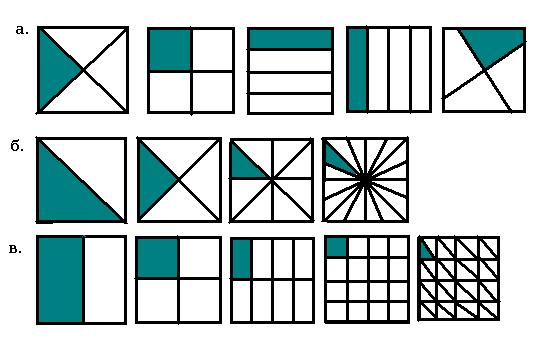

Несколько позже учитель вводит понятие дроби на практической основе. Детям предлагается разделить отрезок на 4 равные части, назвать каждую из них, обвести сначала одну часть, а потом ещё одну. Учитель, сообщает, что получилось собрание долей – оно называется дробью. Затем учитель учит читать и записывать дроби.

Сравнение долей также происходит на наглядно - практической основе в 2 этапа.

1. Практическая работа: детям выдаётся 2 равные полоски бумаги и предлагается на одной закрасить половину, а на другой четверть, а потом сравнить их наложением. Делается вывод, что одна четверть меньше половины.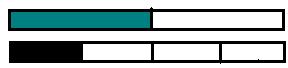

2. Работа с иллюстрацией в учебнике или таблицей на доске.

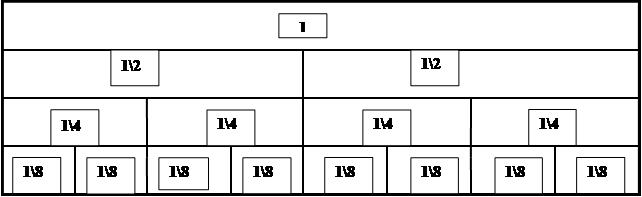
Учащиеся должны выявить название каждой части и визуально сравнить их, причём можно сравнить как доли: 1\2>1\4, так и дроби с одинаковыми знаменателями: 1\8<3\8 и разными знаменателями: 1\2=2\4, 1\4<3\8. Дети находят ответы на вопросы: сколько половин в одной целой, сколько четвёртых долей в одной целой, в половине. В дальнейшем эти задания дети выполняют по представлению, если же появляются затруднения, то опять используется иллюстрация. Формулируются правила: больше та доля, знаменатель которой меньше. Например, 1\2>1\4, так как 2<4. Дроби сравнивают только с одинаковым знаменателем: из двух дробей с одинаковым знаменателем больше та, у которой числитель больше. Например, 3\8>2\8, так как 3>2.

Методика работы с задачами на доли и дроби. В 3 классе рассматриваются задачи на доли (по программе Моро), на доли и дроби (по программе Петерсон).

При знакомстве с задачами этого вида учитель предлагает разделить перегибанием полоску бумаги длиной 12см на 4 равные части и вычислить длину каждой части. Возможны вопросы: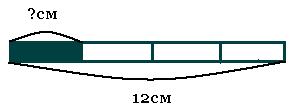

§ Какова длина всей полоски? (12см).

§ На сколько частей надо разделить? (на 4 частей).

§ Какие части: равные по длине или различные? (разделим на 4 равные части).

§ Как можно назвать каждую часть? (четверть).

§ Как узнать длину каждой части? (разделить 12см на 4).

§ Сколько получится? (3см).

§ Проверьте по линейке.

Затем решаются простые задачи на нахождение доли от числа, от величины. Причём по программе Моро в задаче доля задаётся словами: «Длина ленты 10см. Найдите пятую часть этой ленты». Рекомендуется делать чертеж к условию задачи, что позволит наглядно применить конкретный смысл доли для решения задачи.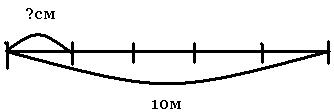

В дальнейшем такие задачи включаются в содержание составных задач. Например: «Найдите площадь четвёртой части квадрата со стороной 9см.» или «В один магазин привезли 28кг яблок, во второй четвёртую часть того, что привезли в первый, а в третий магазин на 12кг больше, чем во второй. Сколько всего килограммов яблок привезли в три магазина вместе?».

Задачи других видов решаются реже, а задачи на дроби и проценты рассматриваются уже в 5-6 классах.

По программе Петерсон рассматриваются задачи всех видов на доли и дроби:

Виды задач	Задачи на доли	Задачи на дроби
Задачи на нахождение части от целого	Длина ленты 10м. Найдите 1\5 этой ленты. 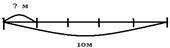10:5=2(м)- длина 1\5 всей ленты.	Длина ленты 10м. Найдите 3\5 этой ле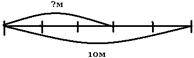нты. 1) 10:5=2(м)- длина 1\5 всей ленты. 2) 2*3=6(м)- длина 3\5 всей ленты.
Задачи на нахождение целого по его части	От ленты отрезали 4м. Найдите длину всей ленты, если отрезали 1\4 ленты. 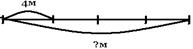4*4=16(м)- длина всей ленты.	От ленты отрезали 9м. Найдите длину всей ленты, если отрезали 3\4 ленты. 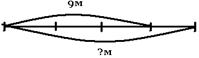1)9:3=3(м)- длина 1\4 всей ленты. 2) 3*4=12(м)- длина всей ленты.
Задачи на нахождение дробного отношения	От ленты длиной 10м отрезали 1м. Какую часть ленты отрезали. Чаще всего такие задачи решаются устно. Или так 1:10=1/10 – всей ленты.	От ленты длиной 10м отрезали 5м. Какую часть ленты отрезали. 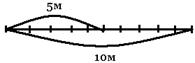Чаще всего такие задачи решаются устно. Или так 5:10=5/10 – всей ленты(сокращать в начальной школе дети не умеют).

Дата добавления: 2014-01-05