Лекция №3. Показатели надежности восстанавливаемого элемента. Комплексные показатели надежности

Показатели надежности восстанавливаемого элемента.

Восстанавливаемый элемент – это такой элемент, работа которого после отказа может быть восстановлена в результате проведения необходимых ремонтных работ. Восстановление приводит к ликвидации последствий отказа. Один и тот же элемент может отказывать несколько раз и после каждого отказа происходит его восстановление и включение в работу.

Функционирование восстанавливаемого объекта за длительный период времени может быть представлено графически потоком отказов и восстановлений либо бесконечно коротких импульсов - при нулевом времени восстановления, или прямоугольных импульсов – при конечном времени восстановления.

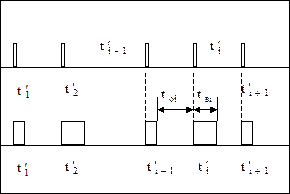
Рис. 6. Поток отказов и восстановлений.

Время между предупредительными ремонтами распадается на отдельные циклы (пери оды): работа и восстановление (ремонт). Каждый цикл состоит из двух интервалов: to – время до отказа и tв – время восстановления.

Потоки отказов обладают рядом свойств.

Поток отказов называется ординарным, если вероятность двух и более отказов за промежуток времени равна нулю, когда длительность этого промежутка времени стремиться к нулю.

Поток отказов называется стационарным, если вероятность появления k отказов на отрезке времени (t, t+∆t) зависит только от ∆t.

Поток отказов называется потоком без последействия, если на любых неперекрещивающихся интервалах времени число событий, появляющиеся в одном из них, не зависят от числа событий, появляющиеся в других.

Ординарные потоки без последействия называются пуассоновскими. Эти потоки могут быть как стационарными, так и нестационарными. Стационарный пуассоновский поток является простейшим.

Энергетические объекты в целом следует считать восстанавливаемыми, хотя могут иметь место случаи, когда отдельные элементы или части объектов на некотором временном интервале можно рассматривать как невосстанавливаемые. Реальные потоки отказов энергетических объектов, как правило, обладают свойствами ординарности и отсутствием последействия, т.е. являются пуассоновскими. Более того, для большинства из них потоки отказов оказываются и стационарными, т.е. простейшими.

Основные допущения анализа потока отказов:

1. Время до отказа (tо) и время восстановления (tв) являются независимыми величинами.

2. Функции распределения времени до отказа (F(t_о1), F(t_о2), F(t_оn)) имеют одинаковый закон распределения, различающиеся лишь только показателями.

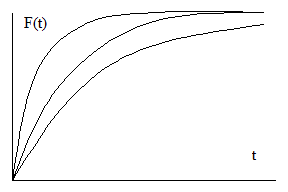
Рис. 7. Функции распределения времени до отказа.

3. Условия эксплуатации на различных участках времени принимаются идентичными.

4. После каждого восстановления элемент обладает характеристиками нового элемента (он возвращается в исходное состояние).

Основные показатели восстанавливаемых элементов:

1. Вероятность безотказной работы на протяжении заданного интервала времени T:

.

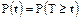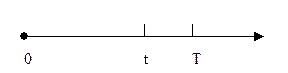
2. Вероятность безотказной работы на протяжении заданного интервала времени T начиная с (k-1) восстановления:

.

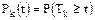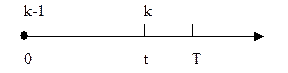
3. Вероятность отказа на протяжении заданного интервала времени T:

.

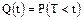4. Вероятность отказа на протяжении заданного интервала времени T начиная с (k-1) восстановления:

.

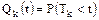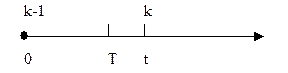
5. Частота отказов :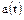

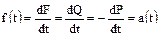
6. Интенсивность отказов :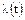

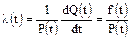
7. Средняя наработка до отказа .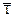

8. Вероятность восстановления 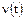- вероятность того, что время восстановления Tв элемента или системы будет меньше времени t:

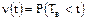
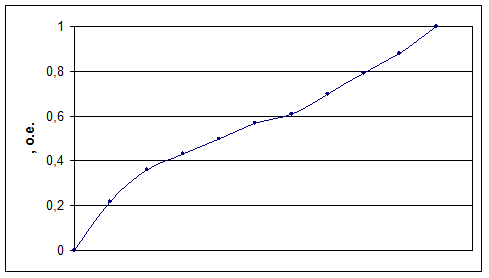
Рис. 8. Вероятность восстановления.

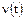обладает свойствами интегральной функции распределения:

·

·

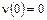
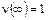
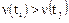· при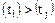

9. Вероятность невосстановления - вероятность того, что время восстановления Tв элемента или системы будет больше или равно времени t:

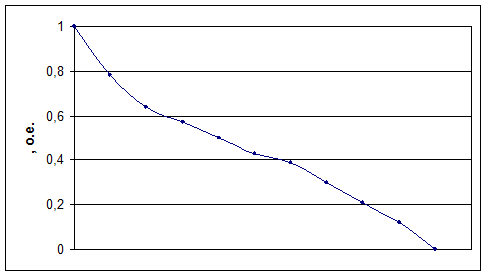
Рис. 9. Вероятность невосстановления.

; .

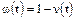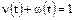10. Частота восстановлений :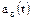

11. Интенсивность восстановления 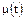в момент времени t, отсчитываемый от начала восстановления, - отношение плотности вероятности восстановления к вероятности невосстановления:

;

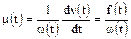
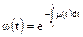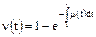
12. Средняя время восстановления 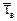- математическое ожидание времени восстановления объекта:

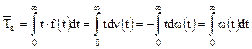
Таким образом, средняя время восстановления графически представляет собой площадь, лежащую под графиком функции .

Для экспоненциального закона распределения времени восстановления, когда , .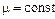

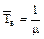13. Параметр потока отказов.

Функционирование восстанавливаемого элемента представляет собой случайный процесс с конечным множеством состояний и непрерывным временем, для которого интервалы t_о,i, t_в,i соответствуют нахождению элемента в рабочем (отказовом) состоянии. Так как для большинства элементов t_о,i>t_в,i, то для описания отказов можно принять более простую модель, а именно случайный ординарный поток однородных событий (отказов).

Обозначим через F(t) распределение случайной величины t_о,i и через 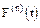распределение случайной величины 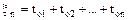, т.е. 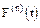представляет собой n-кратную свертку распределения F(t), определяемую по рекуррентной формуле:

.

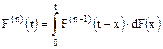К моменту времени t (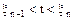) произошло (n-1) отказов элемента. Функция 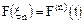однозначно определяет n и более отказов, т.е.:

.

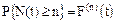Вероятность 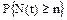полностью определяет закон распределения дискретной случайной величины N(t) для заданного интервала времени [0,t]: 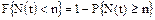. Вероятность появления N(t)=n определяется как:

.

.

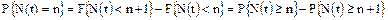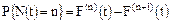Среднее число отказов в интервале времени [0,t]:

.

.

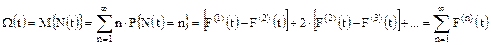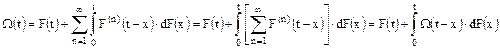Осуществляя предельный переход , получаем функцию , тождественно равную математическому ожиданию числа отказов в единицу времени (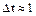). Этот показатель получил название параметра потока отказов:

,

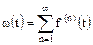где 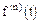- плотность распределения величины .

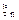Основные комплексные показатели надежности.

1. Коэффициент готовности K_г(t) – определяет вероятность того, что элемент окажется в работоспособном состоянии в произвольный момент времени t.

Стационарный коэффициент готовности (в режиме установившейся эксплуатации):

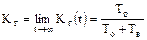
2. Коэффициент простоя K_п(t) – определяет вероятность того, что элемент в произвольный момент времени t будет находиться в состоянии отказа (простоя).

Стационарный коэффициент простоя (в режиме установившейся эксплуатации):

.

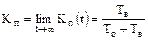
3. Коэффициент технического использования – этот показатель характеризует те же свойства, что и коэффициент готовности, но учитывает дополнительно предупредительные ремонты:

.

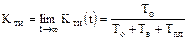4. Средний недоотпуск электроэнергии – характеризует не только все основные свойства надежности системы, но и режим ее загрузки, и представляет собой математическое ожидание недоотпуска электроэнергии потребителям за расчетный период времени.

,

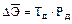где

- дефицит мощности;

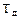- продолжительность существования дефицита мощности.

Эффективность работы системы:

,

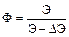где Э – отпущенная потребителю электроэнергия.

5. Экономический ущерб от ненадежности. Этот показатель является наиболее комплексным. Он характеризует интегрально все свойства надежности системы, включая режим ее загрузки и значимость потребителя электроэнергии. Важность каждого потребителя с экономической точки зрения характеризуется величиной удельного ущерба:

.

.

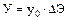Дата добавления: 2014-01-05