Лекция №4. Расчет показателей надежности одноэлементной схемы

Функционирование элементов систем электроснабжения наиболее адекватно можно описать случайным процессом.

Процесс называется марковским, если для каждого момента времени вероятность любого состояния элемента в будущем зависит только от состояния его в настоящий момент времени и не зависит от того, каким образом элемент пришел в это состояние.

Процесс отказов и восстановлений обладает важным свойством: время пребывания элементов в состоянии безотказной работы или восстановления не зависит от того, сколько времени он уже провел в этом состоянии, и распределено по экспоненциальному закону.

Если процесс, протекающий в системе со счетным множеством состояний и непрерывным временем, является марковским, то его можно описать с помощью обыкновенных дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний.

Рассмотрим элемент, который может находиться в двух состояниях: 0 – исправной работы и 1 – отказа (элемент восстанавливается). Определим вероятности состояний p₀(t) и p₁(t) элемента в произвольный момент времени t при различных начальных условиях.

Эту задачу решим при условии, что поток отказов простейший с интенсивностью , закон распределения времени между отказами (частота отказов):

.

Время восстановления описывается также экспоненциальным законом распределения с параметром :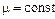

Сначала необходимо составить направленный граф состояний элементов (рис. 1), затем составить систему дифференциальных уравнений для вероятностей состояний.

Рис. 10. Расчетный граф состояний одноэлементной схемы.

Правило составления дифференциальных уравнений:

В левой части каждого уравнения стоит производная 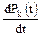, а в правой части – столько членов, сколько ребер связано непосредственно с данным состоянием; если ребро оканчивается в данном состоянии, то член имеет знак плюс, если начинается из данного состояния – знак минус. Каждый член равен произведению интенсивности потока событий, переводящего элемент или систему по данному ребру, и вероятности того состояния, из которого начинается ребро.

.

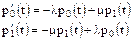Система дифференциальных уравнений может быть использована для определения вероятностей безотказной работы электрических систем, функции и коэффициента готовности, вероятности нахождения в ремонте (восстановлении) среднего времени пребывания системы в любом состоянии на относительно коротких интервалах времени, когда необходим учет начальных условий (состояний элементов).

Решив эту систему уравнений при начальных условиях p₀(0)=1, p₁(0)=0, т.е. предположив, что в момент t=0 элемент находится в рабочем состоянии, получим:

Если в начальный момент времени элемент был в состоянии отказа (восстановления) p₀(0)=0, p₁(0)=1, то

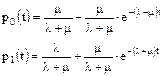
Для установившегося значения вероятности 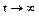, в практических расчетах 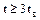коэффициент готовности выражается формулой:

,

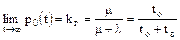а коэффициент вынужденного простоя

.

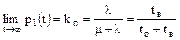Степень затухания экспоненты:

.

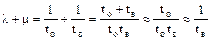Это выражение получено в предположении, что время безотказной работы практически всех элементов электрических систем много больше времени аварийного восстановления. Формулы для практических расчетов можно преобразовать к виду:

при p₀(0)=1, p₁(0)=0:

при p₀(0)=0, p₁(0)=1:

Коэффициент готовности или коэффициент вынужденного простоя можно интерпретировать как среднюю вероятность нахождения систем соответственно в рабочем состоянии и в состоянии отказа. Чем меньше среднее время восстановления элемента, тем больше коэффициент затухания , тем быстрее процесс стремиться к установившемуся значению вероятности, т.е. к установившемся значениям k_г и k_п.

Обычно при определении показателей надежности электроснабжения, связанных с технико-экономической оценкой последствий от недоотпуска электроэнергии для достаточно длительных интервалов времени (сезон, год), без большой погрешности вероятности состояний системы можно считать по установившимся средним вероятностям при . Такого рода режимы с точки зрения надежности называются предельными режимами элемента или системы.

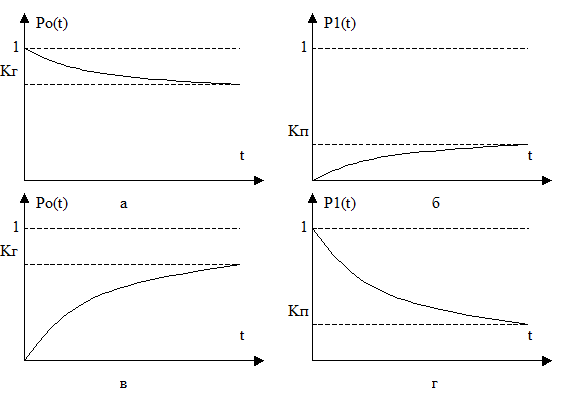
Рис. 11. Зависимости коэффициента готовности и коэффициента вынужденного простоя от времени при различных начальных условиях.

Дата добавления: 2014-01-05