Лекция №8. Вероятности послеаварийных состояний сложных схем электрических соединений. Метод расчета надежности схем на основе формулы полной вероятности

Лекция №7. Режимные характеристики сложных ЭЭС. Метод пересчета параметров режимов и обобщенных параметров при изменении состояния системы. Основные методы структурного анализа систем. Пример расчета структурной и функциональной надежности системы.

Лекция №6. Отражение логики функционирования электрических схем в расчетах показателей надежности. Метод расчета функциональной надежности ЭЭС. Комплексные показатели надежности. Пример расчета недоотпуска электроэнергии.

Лекция №5. Расчет показателей надежности системы, состоящей из последовательных элементов. Расчет показателей надежности системы, состоящей из параллельно соединенных элементов. Расчет показателей надежности системы с произвольным соединением элементов. Расчет показателей надежности с учетом преднамеренных отключений элементов.

Расчет показателей надежности системы, состоящей из последовательных элементов.

Система, состоящая из n последовательных восстанавливаемых элементов, отказывает в тех случаях, когда отказывает любой из элементов. Данная система имеет два состояния: 0 – все элементы в рабочем состоянии, 1 – один из элементов в отказовом состоянии. Система дифференциальных уравнений выглядит следующим образом:

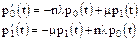
Решив эту систему уравнений при начальных условиях p₀(0)=1, p₁(0)=0, т.е. предположив, что в момент t=0 элемент находится в рабочем состоянии, получим:

Если в начальный момент времени элемент был в состоянии отказа (восстановления) p₀(0)=0, p₁(0)=1, то

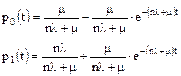
Для установившегося значения вероятности 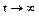, в практических расчетах 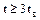коэффициент готовности выражается формулой:

,

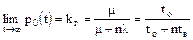а коэффициент вынужденного простоя

.

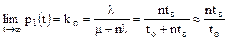Вероятность отказового состояния за время T:

Если элементы неоднородные, т.е. , то

Расчет показателей надежности системы, состоящей из параллельно соединенных элементов.

Параллельное соединение в смысле надежности элементов означает, что при отказе одного из элементов система продолжает выполнять свои функции, т.е. предполагается, что автоматическое резервирование каждого элемента с пропускной способностью, достаточной для полного обеспечения мощности потребителя.

В общем случае, когда система при таком резервировании состоит из n независимых элементов, число возможных состояний системы будет 2n, если считать, что каждый элемент может быть в двух состояниях – рабочем и отказовом – и отказ системы наступает когда все элементы окажутся в отказовом состоянии.

Рассмотрим параллельное соединение двух элементов (две цепи линии электропередачи, двухтрансформаторные подстанции и т.д.). Такая система может находиться в четырех состояниях: 1 – оба элемента в рабочем состоянии; 2 – первый элемент в отказовом состоянии, второй – в рабочем; 3 – второй элемент в отказовом состоянии, первый в рабочем; 4 – оба элемента в отказовом состоянии. Соответствующие вероятности этих состояний будут p₁(t), p₂(t), p₃(t), p₄(t).

Граф переходов для этой системы приведен на рис 12.

Рис. 12. Расчетный граф состояний системы.

Система дифференциальных уравнений, описывающих вероятности состояний во времени следующая:

Решение для стационарного состояния выглядит следующим образом:

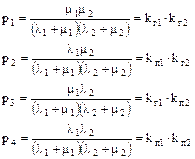
Коэффициент готовности определяется следующим образом:

Коэффициент вынужденного простоя системы:

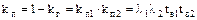
При рассмотрении одноэлементной системы было показано, что коэффициент затухания экспоненты обратно пропорционален времени восстановления элемента:

При условии, что :

,

где

имеет смысл эквивалентного времени восстановления двух параллельно соединенных элементов.

Рассматривая систему с двумя параллельно соединенными элементами как один эквивалентный элемент, можем записать:

,

откуда

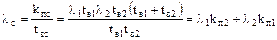
Параметр потока отказов системы из двух резервирующих друг друга элементов равен произведению параметра потока отказов первого на среднюю вероятность отказового состояния второго плюс произведение параметра потока отказов второго на среднюю вероятность отказа первого элемента. Иначе говоря, слагаемые 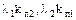имеют смысл удельного числа отказов системы при отказе соответственно первого и второго элементов.

Для определения параметра потока отказов в случае n параллельно соединенных элементов необходимо рассмотреть столько слагаемых, сколько элементов в системе:

.

Расчет показателей надежности системы с произвольным соединением элементов.

Основным методом при исследовании надежности сложных ЭЭС используется метод структурного анализа схем электрических соединений. При расчете показателей надежности с помощью структурных схем анализируются не все возможные состояния схемы, а только состояния отказа того минимального набора элементов, которые приводят к отказу системы относительно рассматриваемого узла (минимальные сечения). Это дает возможность использовать известные приемы расчета, в частности применить формулу для суммы вероятностей совместимых событий – событий отказа сечений.

Вероятность отказа схемы относительно расчетного узла нагрузки:

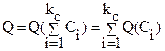
(1.24)

где – количество элементов в сечении, – вероятность отказа i-го сечения:

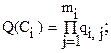
(1.25)

здесь – вероятность отказа j-го элемента i-го сечения; 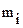– число элементов в i-ом сечении;

(1.26)

В расчет необходимо вводить сечения с числом элементов не более 2-3 в зависимости от необходимой точности расчетов. Здесь k₁, k₂, k₃ – количество одно-, двух и трехэлементных сечений схемы относительно узла нагрузки соответственно.

Определение минимальных сечений по матрице минимальных путей.

Минимальный путь – минимальный набор элементов, которые обеспечивают нормальное функционирование схемы (передачу электроэнергии) от источника питания до узла нагрузки.

Сечения формируются по матрице минимальных путей исходя из следующих соображений: если элемент входит во все пути, то он является одноэлементным сечением, если хотя бы один из двух элементов i и j поочередно входит во все пути и i и j не являются одноэлементными сечениями, то они образуют двухэлементное сечение. Аналогичные рассуждения можно провести относительно трех, четырех и т.д. элементов.

Поэтому для формирования минимальных сечений целесообразно пути представить в виде матрицы путей П, столбцы которой соответствуют элементам схемы, строки – путям. Элементам этой матрицы присваивается значение 1, если элемент входит в соответствующий путь, 0 – если элемент не входит в путь.

По матрице путей можно определить все сечения в схеме относительно рассматриваемого узла нагрузки, анализируя сочетания столбцов матрицы П. Сечения рассматриваются в порядке возрастания числа элементов в них (одноэлементные, двухэлементные, трехэлементные и т.д.).

Для выявления одноэлементных сечений по матрице путей достаточно выявить ее столбец, состоящий из одних единиц (пересечение всех путей в одном элементе). Двухэлементные сечения получаются в результате логического сложения двух любых столбцов матрицы путей (пересечение всех путей в двух элементах). Если в результате получается столбец, состоящий из одних единиц, то эти два элемента образуют двухэлементное сечение. Трехэлементное сечение получается в результате логического сложения трех столбцов (пересечение всех путей в трех элементах) и т.д.

Правила логического сложения:

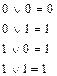
Расчет показателей надежности с учетом преднамеренных отключений элементов.

Вероятность наложения аварийного отключения одного элемента на преднамеренное отключение другого (а не наоборот) определяется с учетом начальных условий. Следовательно, вероятность его аварии за время преднамеренного отключения рассматриваемого элемента меньше средней вероятности его аварийного отключения:

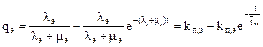
(1.27)

Если продолжительность преднамеренного отключения принять равной , то

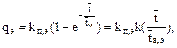
(1.28)

где 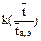- коэффициент, зависящий (рис.13) от соотношения времени аварийного восстановления резервирующего эквивалентного элемента и времени преднамеренного отключения рассматриваемого элемента.

Рис.13. Зависимость понижающего коэффициента k от соотношения времени преднамеренного отключения элемента и эквивалентного времени восстановления оставшейся части системы .

В том случае, если расчеты показателей надежности выполняются на длительных интервалах времени , то в практических расчетах можно не учитывать начальные условия, и фактор уменьшения вероятности совпадения преднамеренного отключения одного элемента и аварийного отключения другого учитывается введением коэффициента

(1.29)

Рис.14. Фрагмент ЭЭС.

На рис.14 изображен фрагмент системы электроснабжения, в которой имеются две параллельные ветви, состоящие из n_в элементов каждая. Один из элементов цепи выводится в плановый ремонт на время T_пр. Вероятность отказа системы до ремонта, во время ремонта и после него описываются следующими выражениями:

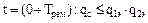
Примерный вид зависимость вероятности отказа системы во времени – на рис. 15.

Рис. 15. Зависимость вероятности отказа системы во времени при отключении одного из элементов для проведения планового ремонта.

Система с последовательным соединением элементов:

В нерезервированных системах электроснабжения для уменьшения вероятности отключенного состояния и уменьшения количества перерывов электроснабжения стремятся по возможности совместить преднамеренные отключения элементов для ремонтов. Коэффициент вынужденного простоя такой системы с учетом преднамеренных отключений определяется по формуле:

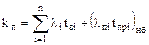
где 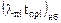- наибольшая вероятность преднамеренного отключения одного из n элементов системы.

Результирующий параметр потока отказов и эквивалентное время восстановления равны:

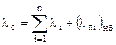
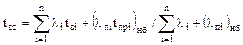
где - наибольшая частота отключения одного из n элементов схемы.

Система с параллельным соединением элементов:

Коэффициент вынужденного простоя:

Параметр потока отказов системы:

.

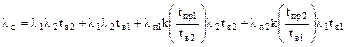Отражение логики функционирования электрических схем в расчетах показателей надежности.

Отказы большей части элементов электрических систем: воздушных и кабельных линий, генераторов, трансформаторов, сборных шин, выключателей и разъединителей (в статическом состоянии) – обычно сопровождаются коротким замыканием. Отказы такого вида не локализуются в самих отказавших элементах, а приводят к необходимости работы релейной защиты и автоматики, воздействующей на коммутационные аппараты (выключатели, в низковольтных сетях – автоматы и предохранители), которые локализуют отказ элемента и ограничивают зону и продолжительность его воздействия на другие элементы.

Коммутационные аппараты могут сами отказывать при необходимости отключения (включения), т.е. при заявке на срабатывание; кроме того, не каждый элемент в электрической системе оборудован с двух сторон автоматическим коммутационным аппаратом, способным локализовать его отказ, поэтому зона его воздействия на систему в зависимости от схемы коммутации может быть весьма значительна, даже при отказе одного независимого элемента. При этом вынужденные отключения других элементов, обусловленные отказом рассматриваемого, классифицируются как зависимые простои. Продолжительность такого рода вынужденных отключений может быть меньше, чем продолжительность аварийного восстановления.

В расчетах структурной надежности предусматривается определение показателей относительно узлов нагрузки системы для состояний их полного отказа, т.е. на основе сечений схемы. Ранее рассматривались только основные сечения схемы, по которым электроэнергия передается непосредственно в узел нагрузки. Взаимосвязь между отказами элементов может порождать ситуации, когда отказы элементов, по которым не передается и не может передаваться электроэнергия в узел нагрузки, также приводят к состоянию полного отказа схемы относительно узла. Минимальные совокупности элементов, по которым непосредственно электроэнергия не передается или передается по части из них, но отказ которых приводит к потере питания узла, называются дополнительными сечениями схемы. Относительно узла формирование условий отказовых состояний в оценках структурной надежности сводится к определению основных и дополнительных сечений схемы.

Для каждого элемента основного сечения определяются все элементы системы, от которых на него может перейти отказ, т.е. вычисляются условные параметры потоков отказов и средние условные вероятности, последние – по продолжительности воздействия зависимых отказов. Затем последовательно вместо элемента основного сечения вводятся элементы, от которых может перейти отказ, тем самым получаются дополнительные сечения. Причем эти элементы вводятся своими условными параметрами потока отказов и соответствующей продолжительностью воздействия. Если основное сечение – одноэлементное, то параметры потоков и вероятности отказов основного и всех дополнительных сечений суммируются. Число дополнительных сечений, как правило, гораздо больше, чем основных, зависимость между отказами элементов как бы осуществляет “размножение” сечений.

Элементы дополнительных сечений образуются из различных списков. По продолжительности воздействия отказов и коэффициентам связи эти списки обозначаются как В, П, А. Так, если элемент не отделен от узла никакими коммутационными аппаратами, то его отказ приводит к отказу узла на продолжительность восстановления t_в, а коэффициент перехода отказа равен единице (список В); если отделен, например, неавтоматическим коммутационным аппаратом, то его отказ приводит к отказу узла на продолжительность оперативных переключений t_п, коэффициент перехода также равен единице (список П); если отделен автоматическим коммутационным аппаратом; то коэффициент перехода равен вероятности отказа q_а выключателя, а продолжительность воздействия t_{п, а} (список А).

При образовании дополнительных сечений с использованием указанных списков необходимо постоянно осуществлять контроль, не является ли полученное сечение основным и не включается ли какой-либо элемент в дополнительное более одного раза.

Метод расчета функциональной надежности ЭЭС.

При отключении отдельных элементов система находится на более низком уровне функционирования по сравнению с нормальным. При этом параметры режимов элементов и систем могут выходить за пределы, допустимые по нормам, что обуславливает отказ, отключение элементов или части системы, т.е. переход системы на еще более низкий уровень функционирования. Чтобы избежать этого, вводятся ограничения по режимам. К ним относятся: форсировка регулирующих и компенсирующих устройств, включение ненагруженных или малонагруженных резервных элементов, коммутационные изменения в схеме и т.д. Если эти мероприятия не обеспечивают введение режима элементов или всей системы в пределы допустимых норм, то отключается часть потребителей.

Рассмотрим определение значения недоотпуска электроэнергии для резервированной системы (рис.16), состоящей из двух элементов, один из которых отключен (j-й элемент), а в другом возникает перегрузка (i-й элемент).

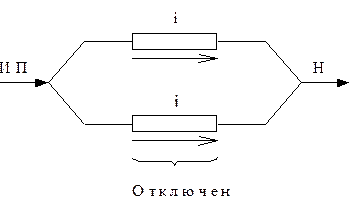
Рис. 16. Схема резервированной сети.

Вероятность перегрузки γ_Ii характеризует относительную долю времени, когда ветвь i будет перегружена. Если считать, что при любой перегрузке сверх расчетной в системе на соответствующее значение будет снижена нагрузка узлов, т.е. ветвь будет полностью разгружена, то недоотпущенная электроэнергия в этом состоянии равна:

где 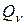– вероятность состояния; ; U_номi – номинальное напряжение в i-й ветви.

Однако в состоянии перегрузки ветвь может быть разгружена не полностью, а лишь на величину 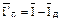, превышающую допустимое значение тока для этой ветви. Тогда недоотпуск электроэнергии потребителям будет минимальным, т.е. эта ситуация соответствует нижней границе недоотпуска:

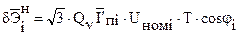
где 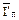при нормальном законе распределения

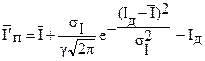
На практике недоотпуск электроэнергии может находиться в диапазоне между верхним и нижним расчетными значениями. Весь анализ будет проводиться только для одного значения недоотпуска электроэнергии, под которым подразумевается его нижняя оценка.

При анализе ремонтных состояний ЭЭС необходимо оценивать функциональную надежность объектов ЭЭС как при "стационарном" состоянии, т.е. при отсутствии отказов элементов, так и при наложении отказов других элементов на плановые ремонты.

Комплексные показатели надежности.

Из комплексных показателей надежности практическое применение имеют два показателя: математическое ожидание недоотпущенной электроэнергии за период времени и экономический ущерб от перерывов электроснабжения.

Математическое ожидание недоотпущенной электроэнергии потребителям узла нагрузки вследствие полного прекращения его питания от системы:

,

(1.35)

или

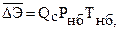
(1.36)

где 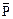– математическое ожидание активной мощности потребителей узла; 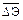– математическое ожидание недоотпуска электроэнергии потребителям; Т – период времени, для которого производится расчет; Р_нб, Т_нб – максимум суммарной мощности узла и время использования максимума мощности соответственно; 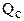– вероятность отказа относительно расчетного узла.

Нарушение нормального функционирования объекта ЭЭС вследствие отказов элементов вызывает экономические санкции к собственнику объекта и как к покупателю электроэнергии и как к продавцу ее.

Как покупатель электроэнергии – вследствие отказа на своем объекте вызывает штрафные санкции со стороны поставщика, обусловленные снижением экономичности работы его оборудования (пережогом топлива, повышением уровня запасом воды на ГЭС, запиранием мощности и т.д.), составляющую Ш_пр.

Как продавец электроэнергии – вследствие недополучения прибыли от продажи электроэнергии (обозначим эту составляющую ПР) и штрафных санкций со стороны покупателя. Эта составляющая называется ущербом у потребителя У. В данном случае величина ущерба принимается равной У_д, согласно условиям договора между поставщиком и потребителем.

В общем случае недополученная прибыль объекта ЭЭС равна:

В зависимости от условий договора объекта ЭЭС с продавцом и покупателем электроэнергии первая и третья составляющие могут принимать любые значения, в том числе и нулевые, но ПР в принципе не может принимать нулевые значения, т.к. электроэнергия относится к физическим субстанциям.

В ряде случаев при оценке необходимой степени обеспечения надежности электроснабжения потребителей пользуются некоторыми средними экономическими показателями. Это связано с тем, что к электрическим сетям присоединяются различные промышленные предприятия, и точная оценка технико-экономического ущерба при перерыве их электроснабжения представляет значительные трудности. Например, при оценке ущерба потребителям можно использовать значение ущерба y₀, отнесенные к 1 кВт*ч недоотпущенной электроэнергии.

При этом в случае прекращения электроснабжения потребителей ущерб потребителям равен:

У=у0Энпр.

Удельный экономический ущерб y₀ может многократно превышать стоимость недоотпущенной потребителю электроэнергии.

Пример расчета недоотпуска электроэнергии для резервированной схемы.

Исходные данные:

Нагрузка потребителя электроэнергии изменяется по равномерному закону в диапазоне от 20 до 100 МВт. Допустимая на один элемент – 45 МВт.

Показатели надежности элементов:

Показатель	Значение
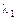, 1/год
, 1/год
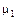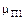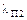, 1/год
, 1/год
, 1/год
, 1/год
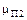, 1/год
, 1/год

Требуется определить недоотпуск электроэнергии потребителю за год.

1. Расчет показателей структурной надежности системы:

Вероятность отказа элементов:

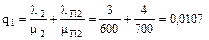
Понижающие коэффициенты для учета преднамеренных отключений элементов:

Вероятность полного прекращения питания потребителя:

2. Расчет показателей функциональной надежности системы:

2.1. Все элементы находятся в работоспособном состоянии:

, ,

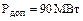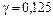
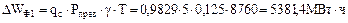
2.2. Первый элемент отказал или находится в плановом ремонте:

, ,

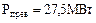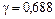
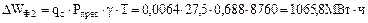
2.3. Второй элемент отказал или находится в плановом ремонте:

, ,

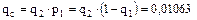
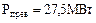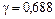
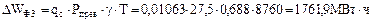
Суммарный недоотпуск электроэнергии потребителям:

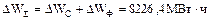
Режимные характеристики сложных ЭЭС.

Для расчетов токораспределения и напряжений узлов используются обобщенные параметры схем, матрица узловых сопротивлений 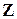, коэффициентов распределения C. Из теории электрических сетей известно, что токи ветвей и напряжения узлов относительно напряжения базового узла определяется следующим образом:

где 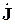– матрица задающих токов узлов (положительное направление принимается к узлу).

Все обобщенные параметры целесообразно выразить через матрицу узловых сопротивлений Z, которая получается в результате обращения матрицы узловых проводимостей Y_у:

Z=Yу^-1=(MуMt)^-1,

где M, у – соответственно первая матрица инциденций и матица проводимостей ветвей (обычно диагональная); t – знак транспонирования.

Порядок обращаемой матрицы равен числу независимых узлов схемы n. Матрица коэффициентов распределения:

С=ГZ.

Таким образом, исходной информацией, характеризующей схему, являются: полностью заполненная матрица узловых сопротивлений Z размером n X n (в общем случае она получается обращением матрицы Y_у порядка n); слабозаполненная матрица Г_t размером n X m, где m – число ветвей схемы (она легко получается из матрицы М_t заменой элементов +1 и –1 на значения соответствующих проводимостей ветвей у с сохранением знаков, отражающих выбранные направления); диагональная матрица у (если не учитываются взаимные индуктивности между ветвями).

Метод пересчета параметров режимов и обобщенных параметров при изменении состояния системы.

Для оценки недоотпуска электроэнергии при любых моделях схем и режимов электропотребления необходим анализ значительного числа состояний. При этом оказывается нерациональным расчет параметров режимов с получением матрицы Z ^(r) для каждого состояния обращением матрицы Y ^(r). Основные причины этого:

- конфигурация систем в ремонтных состояниях незначительно отличаются одна от другой, так как отключаются и включаются одновременно обычно небольшое количество элементов;

- обращение матрицы Y _у^(r) является очень трудоемкой операцией, к тому же для каждого состояния необходима информация о всех элементах полностью заполненной матрицы Z ^(r), в противном случае не удается выявить элементы (узлы и ветви) с недопустимыми параметрами режимов.

С ростом размера анализируемой системы нерациональность такого подхода трансформируется, по существу, в невозможность практической реализации с помощью современных средств вычислительной техники.

Необходим метод пересчета матрицы Z, при котором выполнялись бы следующие требования:

- использование единой информации о режимах и схеме для пересчета параметров режимов при большом количестве состояний системы. В качестве такой информации целесообразно использовать информацию для нормального состояния системы;

- возможность ускоренного пересчета параметров режима и обобщенных параметров схемы с выявлением тех элементов, режимы которых выходят за допустимые пределы;

- ускоренный пересчет любой части матриц обобщенных параметров без пересчета всей матрицы. Это имеет существенное значение при анализе схем большого размера.

При изменении состояния системы нагрузки отключаемых или включаемых ветвей, если узлы сохраняются в схеме, перераспределяются между оставшимися в работе, т.е. происходит приращение нагрузок ветвей.

Если, например, отключаются r ветвей, то нагрузки оставшихся ветвей 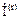можно представить в виде:

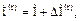
где – приращение нагрузок ветвей, обусловленное изменением схемы и перераспределением нагрузок коммутируемых ветвей.

Значение этого приращения для каждой ветви зависит от нагрузки 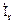отключаемых ветвей в доремонтном состоянии, схемы системы и обобщенных параметров, поэтому:

,

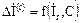где g_I – матрица распределения нагрузок отключаемых или включаемых ветвей, определяемая по изменению обобщенных параметров схемы.

Аналогичные рассуждения можно провести относительно напряжений узлов V. При отключении r ветвей

,

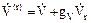где g_V – матрица распределения напряжений узлов, инцидентных отключаемым или включаемым ветвям, определяемая по изменению обобщенных параметров схемы;

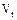– матрица разности напряжений узлов, инцидентных коммутируемым ветвям в доремонтном состоянии схемы.

Матрицы g_V и g_I (обобщенные параметры изменения схем) зависят только от исходных обобщенных параметров схем и изменений конфигурации.

В общем случае ремонтное состояние системы может реализовываться не только отключением r ветвей, но и включением s ветвей, так как при ремонтах производятся переключения в схеме.

Основным обобщенным параметром схемы системы, по которому определяются режимы нагрузок ветвей и напряжений узлов, является матрица узловых сопротивлений. Матрицы g_V и g_I получаются в результате пересчета элементов матрицы Z.

Анализ числовых значений матриц 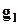и 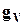позволяет выявить зону влияния нагрузок отключаемых ветвей на оставшиеся в работе элементы схемы и наметить мероприятия для введения режимов в допустимые пределы в каждом состоянии.

Основные методы структурного анализа систем.

При оценке надежности ЭЭС невозможно обойтись без специальных методов и алгоритмов анализа структуры системы, на основе которых выявляются основные и дополнительные сечения схемы, базовые пути питания потребителей электроэнергии, анализируется схема выдачи мощности электрическими станциями и др. В основном все алгоритмы анализа системы построены на графах.

Рассмотрим два основных метода - поиск в ширину и поиск в глубину, на основании которых можно решить любой круг задач, связанных с анализом графов.

Поиск в ширину:

Пусть задан граф G=(V,E) и фиксированная начальная вершина s. Алгоритм поиска в ширину перечисляет все достижимые из s (если идти по ребрам) вершины в порядке возрастания расстояния от s. Расстоянием считается длина (число ребер) кратчайшего пути. В процессе поиска из графа выделяется часть, называемая “деревом поиска в ширину” с корнем s. Она содержит все достижимые из s вершины (и только их). Для каждой из них путь из корня в дереве поиска будет одним из кратчайших путей (из начальной вершины) в графе. Алгоритм применим как к ориентированным, так и к неориентированным графам.

Название объясняется тем, что в процессе поиска мы идем вширь, а не вглубь (сначала просматриваем все соседние вершины, затем соседей соседей и т.д.).

Построенный таким образом подграф G_π графа G представляет собой дерево, в котором для каждой вершины ν имеется единственный простой путь из s в ν. Этот путь будет кратчайшим путем из s в ν в графе G.

Поиск в глубину:

Стратегия поиска в глубину такова: идти “вглубь”, пока это возможно (есть не пройденные исходящие ребра), и возвращаться и искать другой путь, когда таких ребер нет. Так делается, пока не обнаружены все вершины, достижимые из исходной. (Если после этого остаются необнаруженные вершины, можно выбрать одну из них и повторять процесс, и делать так до тех пор, пока мы не обнаружим все вершины графа).

Как и при поиске в ширину, впервые обнаружив вершину ν, смежную с u, мы отмечаем это событие. Получается дерево – или несколько деревьев, если поиск повторяется из нескольких вершин. Говоря дальше о поиске в глубину, всегда предполагается, что поиск повторяется.

Как алгоритм поиска в ширину, так и алгоритм поиска в глубину служат для формирования кратчайших путей из одной вершины графа в другую. Набор кратчайших путей, например, от узла нагрузки до источника(ов) питания необходим для определения минимальных сечений относительно рассматриваемой точки. Простейший способ определения основных сечений схемы – вынужденное пересечение нескольких путей в одном, двух и т.д. элементах. Так, например, если два независимых пути пересекаются в одном элементе, то этот элемент является одноэлементным сечением; если четыре независимых пути пересекаются в двух элементах, то эти элементы формируют двухэлементное сечение относительно узла нагрузки и т.д.

Математическое ожидание недоотпуска электроэнергии в послеаварийных состояниях существенно зависит не только от вероятностей и значений превышения допустимых параметров режима, но и от вероятностей послеаварийных состояний системы.

Каждый элемент может не выполнять свои функции вследствие отказа в нем самом, либо в результате вынужденного простоя из-за отказа других элементов, электрически связанных с ним, либо вследствие его преднамеренного отключения. Количество возможных сочетаний причин отключения элемента от схемы может быть значительным даже для схем небольшого размера, поэтому целесообразно эту задачу решать с помощью ЭВМ.

Для сокращения размерности задачи в сложной схеме целесообразно выделить расчетные элементы, состоящие, как правило, из группы реальных элементов. Затем с использованием методов структурного анализа определяется состав путей перехода отказов от других элементов вследствие электрической и других видов связи с ними, т.е. формируются списки:

· элементов, не отделенных от расчетного никакими коммутационными аппаратами (список В); вынужденный простой расчетного элемента при отказе таких элементов будет ликвидирован за время аварийного восстановления отказавшего элемента t_в;

· элементов, отделенных от расчетного неавтоматическими нормально включенными коммутационными аппаратами (список П); вынужденный простой расчетного элемента при отказе таких элементов будет ликвидирован за время, равное продолжительности оперативных переключений t_п;

· элементов, отделенных от расчетного автоматическими коммутационными аппаратами (список А); при отказе таких элементов вынужденный простой будет ликвидирован за время, равное продолжительности оперативных переключений t_па; но при условии отказа автоматического коммутационного аппарата с вероятностью q_а при заявке на срабатывание.

Иначе говоря, определяется состав множества путей перехода отказов. При этом параметр потока переходов отказов по j-му пути от i-го элемента

где 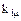- коэффициент перехода отказов (для неавтоматических коммутационных аппаратов он равен 1; для автоматических – вероятности отказа при заявке на срабатывание; - число элементов в пути перехода отказов).

Параметр потока отказов по множеству путей равен сумме параметров потока отказов по отдельным путям.

Параметр потока отказов k-го расчетного элемента:

,

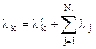где - число путей переходов отказов; 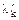- параметр потока отказов собственно k-го элемента.

Вероятность отказа (относительная длительность вынужденного простоя) расчетного элемента в общем случае:

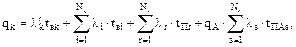
где Nв, Nп, Na – количество элементов соответственно в списках В, П, А.

Дата добавления: 2014-01-05