Цилиндрические и конические поверхности

1. Цилиндрические поверхности.

Цилиндрической поверхностью называется поверхность, образо­ванная параллельными между собой прямыми , называемыми, ее образующими.

Если какая-нибудь плоскость, пересекающая все образующие цилиндрические поверхности, пересекает ее по линии С, то эта линия называется направляющей этой цилиндрической поверх­ности.

Теорема 1. Если в пространстве введена общая декартова система координат, и уравнение F (x,у)=0 в плоскости хОу является уравнением некоторой линии С, то это уравнение в пространстве есть уравнение цилиндрической поверх­ности П с направляющей

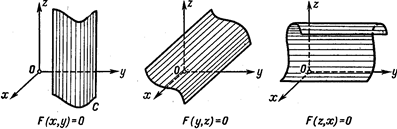
Рис.61 Рис. 62 Рис. 63

линией С, а образующие параллельны оси Оz (рис. 61).

Доказательство. Точка М (х,у,z) лежит на цилиндри­ческой поверхности П тогда и только тогда, когда проекция М' (х,у, 0) точки М на плоскость хОу параллельно оси Оz лежит на линии С, т. е. тогда и только тогда, когда выполняется урав­нение F (х,у) =0.

Теорема 2 (обратная). Если П - цилин-дрическая поверхность, направляющей которой является плоская линия С, а образующие поверхности П параллельны некоторой прямой , не лежащей в плоскости линии С, то существует система координат, в которой уравнение поверхности П имеет вид F (x, у)=0.

Доказательство. Введем общую декартову систему коор­динат Охуz, совмещая плоскость хОу с плоскостью, в которой расположена линия С, и принимая за ось Оz - ось, параллельную прямой l. Пусть F (х,у) = 0 уравнение линии С в плоскости хОу. На основании предыдущей теоремы это уравнение в пространстве во введенной системе координат является цилиндрической поверхностью П.

Замечание 1. Аналогичные заключения имеют место для уравнений вида F (у,z)=0 и F (z, х) = 0 (рис. 62 и 63).

Замечание 2. Если линия С на плоскости хОу задана параметрическими уравнениями х=х (и), у=у (и), то параметри­ческие уравнения поверхности П с направляющей С, образующие которой параллельны оси Оz, можно записать в виде х=х (и), у=у (и), z= .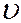

Пример 1. Уравнение 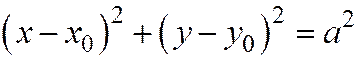в декартовой прямоугольной системе хОу на плоскости является уравнением окружности С с центром в точке (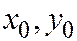), и радиусом а. Если ввести ось Оz, не лежащую в плоскости хОу, то в полученной общей декартовой системе координат Oxyz это же уравнение в пространстве является уравнением на­клонного цилиндра, образующие которого параллельны оси Оz, а направляю­щая - окружность С. Сечения этой цилиндрической поверхности плоскостями, параллельными плоскости хОу - окружности, по-лученные переносом окружности С вдоль оси Оz.

Пример 2. Уравнение , где , в декартовой прямоугольной системе координат хОу на плоскости является уравнением параболы С. Присоединяя ось Оz, не лежащую в плоскости хОу, получим пространственную систему координат Охуz, относительно которой уравнение является уравнением цилиндра, направляющая которого - парабола С, а образу-ющие параллельны оси Оz (параболический цилиндр).

2. Конические поверхности.

Определение 1. Конической поверхностью называется поверх­ность, образованная множеством прямых 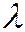, проходящих через одну точку S, называемую вершиной этой поверхности. Прямые называются образующими конической поверхности.

Если какая-нибудь плоскость, не проходящая через вершину конической поверхности и пересекающая все ее образующие, пересекает коническую поверхность по линии С, то эта линия называется направляющей конической поверхности.

Определение 2. Функция F(x,у,z) называется однородной, если она обладает следующими свойствами:

1) если точка (х,у,z) входит в область опреде-ления функции F(x,у,z), то точка (kx,ky,kz), где k-любое число, также входит в область определения этой функции;

2) существует такое число п, что для любой точки (х,у,z) из области определения функции F(х,у,z) и для любого числа k выполняется соотношение

F (kx,ky,kz) =k ⁿ F (x,у,z).

Число п называется показателем однородности.

Теорема. Если уравнение F (х,у,z) = 0, где F (х,у,z) - однородная функция, в декартовой системе коор­динат является уравнением поверхности К, то эта поверхность коническая, причем вершина конуса лежит в начале координат.

Доказательство. Если точка М (х,у,z) (отличная от начала координат) лежит на поверхности, заданной уравнением F (x,у,z) = 0, то на той же поверхности лежит точка (kx,ky,kz), где k - любое число. В самом деле,

F (kx,ky,kz) =kⁿF (x,у,z)=0.(1)

Если k принимает все действительные значения, то точка (kx,ky,kz) описывает всю прямую, проходящую через точку М и начало координат О, так как точка (kx,ky,kz) в случае 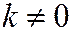делит направленный отрезок в отношении 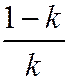. Действи­тельно, вычисляя координаты делящей точки по формулам § 13, получим.

Начало координат (в случае п > 0) также принадлежит поверх­ности, заданной уравнением F (х,у,z)=0, так как, полагая в соотношении (1) k =0, получим F (0,0,0)=0.

Таким образом, если на поверхности К лежит какая-нибудь точка, не совпадающая с началом координат, то на ней лежит вся прямая, проходящая через эту точку и начало координат. Итак, поверхность образована прямыми, проходящими через начало координат, т. е. является конической поверхностью с вершиной в начале координат.

Дата добавления: 2014-01-05