
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Деление отрезка в данном отношении. Постановка задачи. Пусть в пространстве (на плоскости) даны две различные точки A и B
|
|
|
|
Постановка задачи. Пусть в пространстве (на плоскости) даны две различные точки A и B. Тогда однозначно определена проходящая через них прямая l. Возьмём теперь произвольную точку C на этой прямой с единственным условием C ≠ B. Тогда вектор  будет коллинеарен вектору
будет коллинеарен вектору 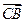 , и при этом
, и при этом 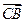 ≠ 0. В силу предложения о двух коллинеарных векторах из п. 1.1.2нцао отрезка.
≠ 0. В силу предложения о двух коллинеарных векторах из п. 1.1.2нцао отрезка.
ваются. (лекция № 2 от 08.09.09) существует, и притом единственное, число λ такое, что  = λ
= λ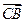 .
.
Определение. В описанной ситуации говорят, что точка C делит отрезок AB (но не BA!) в отношении λ.
Иногда это выражают в виде равенства
λ = 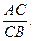
Надо только иметь в виду, что в этой формуле берутся не длины, а величины отрезков AC и CB. Если отрезки AC и CB одинаково направлены, то этому отношению присваивается знак плюс, если противоположно направлены − знак минус. Так получается варьянт определения, эквивалентный вышеприведённому.
Заметим, что λ положительно, если точка C лежит на прямой l между точками A и B, и оно отрицательно, если точка C лежит на прямой l вне отрезка AB. Если C = A, то λ = = 0. При λ = 1 имеем середину отрезка. Можно доказать, что λ принимает любые значения, кроме −1 (мы этого доказывать не будем).
Задача. Даны координаты точек A и B и число λ. Требуется найти координаты точки C.
Решение. Сначала решим задачу в векторном виде. Пусть O − сначала произвольная точка пространства (плоскости). Имеем:
 +
+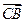 =
=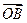 ;
;
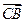 =
=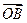 −
− ;
;
 =
=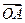 +
+ =
=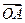 + λ
+ λ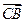 =
=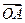 + λ(
+ λ(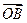 −
− );
);
(1 + λ)  =
=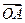 + λ
+ λ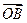 ;
;
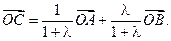
(Как было сказано выше, λ не может равняться −1.) Последнее равенство можно считать решением нашей задачи в векторном виде.
Пусть теперь O − не произвольная точка, а начало координат. Пусть также
A = (x 1, y 1, z 1), B = (x 2, y 2, z 2), C = (x *, y *, z *).
Тогда
x * = absc. C = absc.  =
= =
=
=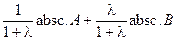 =
=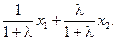
Аналогично для других координат. Окончательно имеем формулы:
x * =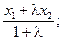
y * =
z * =
Для середины отрезка, т. е. для случая λ = 1, имеем особенно простые формулы:
x * =
y * =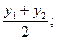
z * =
т. е. мы доказали
Предложение. Координаты середины отрезка суть средние арифметические соответствующих координат концов этого отрезка.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 607; Нарушение авторских прав?; Мы поможем в написании вашей работы!