Операторы

В информационных системах это правило, переводящее некоторый объект или систему из одного состояния в другое, элемент решения задачи. В качестве оператора, например, может выступать модель, реализующая некоторое преобразование над входными данными.

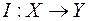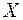Рассмотрим функциональное отображение , где и 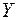─ множества функций: .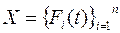

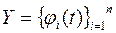В этом случае отображение 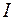называется оператором.

Оператор представляет собой множество упорядоченных пар, первый и второй элементы которых представляют собой функции:

Таким образом, под операторами понимают отображение, ставящее в соответствие функции другую функцию («оператор на пространстве функций» звучит лучше, чем «функция от функции»).

.

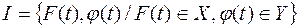В математике и технике широко применяется условная форма записи операторов, аналогичная алгебраической символике. Такая символика в ряде случаев позволяет избежать сложных преобразований и записывать формулы в простой и удобной форме. Аргументы оператора называются операндами, число операндов называется арностью оператора (например, одинарный, бинарный). Написание операторов можно систематизировать следующим образом:

- префиксная: где первым идёт оператор и операнды следом, например:

;

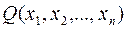- постфиксная: если символ оператора следует за операндами, например:

;

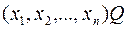- инфиксная: оператор вставляется между операндами, применяется преимущественно с двоичными операторами:

;

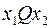- позиционная: знак оператора опускается, оператор присутствует неявно. Чаще всего не пишется оператор произведения (переменных, численного значения на физическую единицу, матриц, композиция функций), например, 3 кг. Такая способность одного оператора действовать над разнородными сущностями достигается перегрузкой операторов;

- подстрочная или надстрочная слева или справа; главным образом используется для операций возведения в степень и выбора элемента вектора по индексу.

Дата добавления: 2014-01-05