Производные и дифференциалы высших порядков

Частные производные функции z = f (x,y) являются, в свою очередь, функциями переменных х и у. Следовательно, можно найти их частные производные по этим переменным. Обозначим их так:

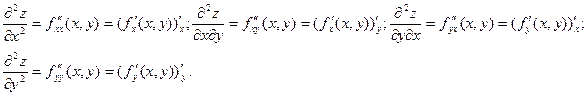
Таким образом, получены четыре частные производные 2-го порядка. Каждую из них можно вновь продифференцировать по х и по у и получить восемь частных производных 3-го порядка и т.д. Определим производные высших порядков так:

Определение 3.2. Частной производной n -го порядка функции нескольких переменных называется первая производная от производной (n – 1)-го порядка.

Частные производные обладают важным свойством: результат дифференцирования не зависит от порядка дифференцирования (например, 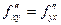). Докажем это утверждение.

Теорема 3.3. Если функция z = f (x,y) и ее частные производные 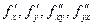определены и непрерывны в точке М (х, у) и в некоторой ее окрестности, то в этой точке

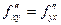(3.3)

Доказательство.

Рассмотрим выражение 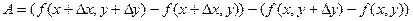и введем вспомогательную функцию 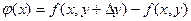. Тогда

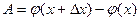. Из условия теоремы следует, что 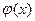дифференцируема на отрезке [ x, x+ Δ x ], поэтому к ней можно применить теорему Лагранжа: 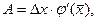где

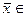[ x, x+ Δ x ]. Но 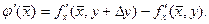Так как в окрестности точки М определена 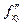, 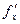дифференцируема на отрезке [ y, y + Δ y ], поэтому к полученной разности вновь можно применить теорему Лагранжа: 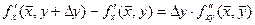, где 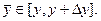Тогда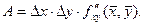

Изменим порядок слагаемых в выражении для А:

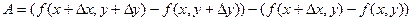и введем другую вспомогательную функцию 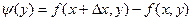, тогда 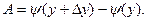Проведя те же преобразования, что и для 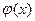, получим, что 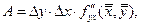где 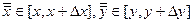. Следовательно,

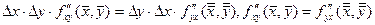. В силу непрерывност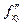и и 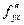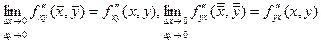. Поэтому, переходя к пределу при 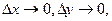получаем, что 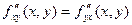, что и требовалось доказать.

Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.

Дифференциалы высших порядков.

Определение 3.2. Дифференциалом второго порядка функции u = f (x, y, z) называется

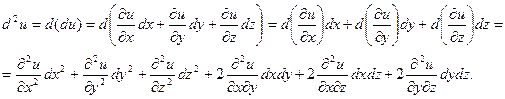
Аналогично можно определить дифференциалы 3-го и более высоких порядков:

Определение 3.3. Дифференциалом порядка k называется полный дифференциал от дифференциала порядка (k – 1): d ^k u = d (d ^{k- 1} u).

Свойства дифференциалов высших порядков.

1. k -й дифференциал является однородным целым многочленом степени k относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные k -го порядка, умноженные на целочисленные постоянные (такие же, как при обычном возведении в степень):

.

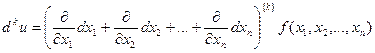1. Дифференциалы порядка выше первого не инвариантны относительно выбора переменных.

Лекция 4.

Дата добавления: 2014-01-05