
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 7. Комплексные числа, их изображение на плоскости
|
|
|
|
Комплексные числа, их изображение на плоскости. Алгебраические операции над комплексными числами. Комплексное сопряжение. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Корни из комплексных чисел. Показательная функция комплексного аргумента. Формула Эйлера. Показательная форма комплексного числа.
При изучении одного из основных приемов интегрирования: интегрирования рациональных дробей – требуется для проведения строгих доказательств рассматривать многочлены в комплексной области. Поэтому изучим предварительно некоторые свойства комплексных чисел и операций над ними.
Определение 7.1. Комплексным числом z называется упорядоченная пара действительных чисел (а,b): z = (a,b) (термин «упорядоченная» означает, что в записи комплексного числа важен порядок чисел а и b: (a,b)≠(b,a)). При этом первое число а называется действительной частью комплексного числа z и обозначается a = Re z, а второе число b называется мнимой частью z: b = Im z.
Определение 7.2. Два комплексных числа z1 = (a1, b1) и z2 = (a2, b2) равны тогда и только тогда, когда у них равны действительные и мнимые части, то есть a1 = a2, b1 = b2.
Действия над комплексными числами.
1. Суммой комплексных чисел z1 = (a1, b1) и z2 = (a2, b2) называется комплексное число z = (a,b) такое, что a = a1 + a2, b = b1 + b2. Свойства сложения: а) z1 + z2 = z2 + z1; б) z1 + (z2 + z3) = (z1 + z2) + z3; в) существует комплексное число 0 = (0,0): z + 0 = z для любого комплексного числа z.
2. Произведением комплексных чисел z1 = (a1, b1) и z2 = (a2, b2) называется комплексное число z = (a,b) такое, что a = a1a2 – b1b2, b = a1b2 + a2b1. Свойства умножения: а) z1z2 = z2z1; б) z1 (z2 z3) = (z1 z2) z3, в) (z1 + z2) z3 = z1 z3 + z2 z3.
Замечание. Подмножеством множества комплексных чисел является множество действительных чисел, определяемых как комплексные числа вида (а, 0). Можно убедиться, что при этом определение операций над комплексными числами сохраняет известные правила соответствующих операций над действительными числами. Кроме того, действительное число 1 = (1,0) сохраняет свое свойство при умножении на любое комплексное число: 1∙ z = z.
Определение 7.3. Комплексное число (0, b) называется чисто мнимым. В частности, число (0,1) называют мнимой единицей и обозначают символом i.
Свойства мнимой единицы:
1) i∙i=i ² = -1; 2) чисто мнимое число (0, b) можно представить как произведение действительного числа (b, 0) и i: (b, 0) = b∙i.
Следовательно, любое комплексное число z = (a,b) можно представить в виде: (a,b) = (a,0) + (0,b) = a + ib.
Определение 7.4. Запись вида z = a + ib называют алгебраической формой записи комплексного числа.
Замечание. Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры.
Определение 7.5. Комплексное число 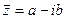 называется комплексно сопряженным числу z = a + ib.
называется комплексно сопряженным числу z = a + ib.
3. Вычитание комплексных чисел определяется как операция, обратная сложению: z = (a,b) называется разностью комплексных чисел z1 = (a1, b1) и z2 = (a2, b2), если a = a1 – a2, b = b1 – b2.
4. Деление комплексных чисел определяется как операция, обратная умножению: число z = a + ib называется частным от деления z1 = a1 + ib1 и z2 = a2 + ib2 (z2 ≠ 0), если z1 = z∙z2. Следовательно, действительную и мнимую части частного можно найти из решения системы уравнений: a2 a – b2 b = a1, b2 a + a2 b = b1.
Геометрическая интерпретация комплексных чисел.
Комплексное число z = (a,b) можно представить в виде точки на плоскости с координатами (a,b) или вектора с началом в начале координат и концом в точке (a,b).
При этом модуль полученного вектора называется модулем комплексного числа, а угол, образованный вектором с положительным направлением оси абсцисс,- аргументом числа. Учитывая, что a = ρ cos φ, b = ρ sin φ, где ρ = | z | - модуль z, а φ = arg z – его аргумент, можно получить еще одну форму записи комплексного числа:
Определение 7.6. Запись вида
z = ρ (cos φ + i sin φ) (7.1)
называется тригонометрической формой записи комплексного числа.
В свою очередь, модуль и аргумент комплексного числа можно выразить через а и b: 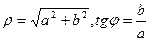 . Следовательно, аргумент комплексного числа определен не однозначно, а с точностью до слагаемого, кратного 2π.
. Следовательно, аргумент комплексного числа определен не однозначно, а с точностью до слагаемого, кратного 2π.
Легко убедиться, что операция сложения комплексных чисел соответствует операции сложения векторов. Рассмотрим геометрическую интерпретацию умножения. Пусть 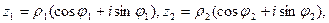 тогда
тогда 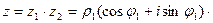
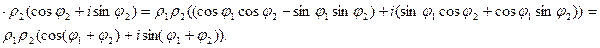
Следовательно, модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент – сумме их аргументов. Соответственно, при делении модуль частного равен отношению модулей делимого и делителя, а аргумент – разности их аргументов.
Частным случаем операции умножения является возведение в степень:
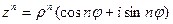 (7.2)
(7.2)
- формула Муавра.
Используя полученные соотношения, перечислим основные свойства комплексно сопряженных чисел:
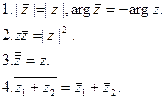
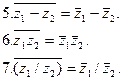
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 457; Нарушение авторских прав?; Мы поможем в написании вашей работы!