Относительно производной

Дифференциальные уравнения первого порядка, разрешенные

Рассмотрим уравнение вида 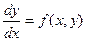. (16.2)

Можно показать, что общее решение такого уравнения зависит от одной произвольной постоянной. С геометрической точки зрения уравнение (16.2) устанавливает зависимость между координатами точки на плоскости и угловым коэффициентом 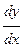касательной к графику решения в той же точке. Следовательно, уравнение (16.2) определяет некоторое поле направлений, и задача его решения состоит в том, чтобы найти кривые, называемые интегральными кривыми, направление касательных к которым в каждой точке плоскости совпадает с направлением этого поля.

Примеры.

1) 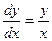. В каждой точке, кроме начала координат, угловой коэффициент к искомой интегральной кривой равен 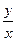, то есть тангенсу угла, образованного с осью О х прямой, проходящей через данную точку и начало координат. Следовательно, интегральными кривыми в данном случае будут прямые вида у = сх (рис.1).

у

у

х

х

Рис. 1. Рис. 2.

2) 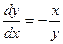. В этом случае касательная в каждой точке плоскости перпендикулярна направлению прямой, проходящей через эту точку и начало координат, так как угловые коэффициенты этих прямых удовлетворяют условию ортогональности: 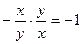. Поэтому направление касательной в данной точке совпадает с направлением касательной к окружности с центром в начале координат, на которой лежит выбранная точка. Такие окружности и являются интегральными кривыми данного уравнения (рис. 2).

Часто для построения интегральных кривых удобно предварительно найти геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами.

Пример.

Изоклины уравнения 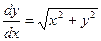задаются уравнениям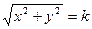и или 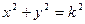, так как на каждой изоклине производная 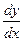должна сохранять постоянное значение. Полученные уравнения задают семейство концентрических окружностей с центром в начале координат, а угловой коэффициент касательной к интегральной кривой равен радиусу проходящей через данную точку окружности.

Задача Коши для уравнения первого порядка.

Как уже было сказано, общим решением уравнения (16.2) является все множество функций, обращающих при подстановке рассматриваемое уравнение в тождество. Пусть теперь требуется найти решение этого уравнения, удовлетворяющее условию

у (х₀) = у₀, (16.3)

называемому начальным условием. Если общее решение уравнения (16.2) задается формулой у = φ (х, С), (16.4)

то значение постоянной С, соответствующее поставленному начальному условию, можно определить, подставив в равенство (16.4) х = х₀ и у = у₀.

Определение 16.3. Задача выбора из общего решения (16.4) уравнения (16.2) решения, удовлетворяющего начальному условию (16.3), называется задачей Коши, а выбранное решение называется частным решением уравнения (16.2).

Замечание. Если воспринимать множество всех решений уравнения (16.2) как множество интегральных кривых на плоскости, то ставится задача поиска той из них, которая проходит через точку с координатами (х₀, у₀). Выясним, при каких условиях такая кривая существует и является единственной.

Дата добавления: 2014-01-05