Теорема существования и единственности задачи Коши

Рассмотрим предварительно метод приближенного решения дифференциальных уравнений, обоснование которого будет дано в приведенной ниже теореме.

Метод Эйлера.

Метод Эйлера заключается в том, что искомая интегральная кривая уравнения (16.2), проходящая через точку (х₀, у₀), заменяется ломаной, каждое звено которой касается интегральной кривой в одной из своих граничных точек (рис. 3).

у

h

h

y₀ y₁ y₂

O x₀ x₁ x₂ x

Рис. 3

Пусть требуется найти приближенное значение искомого решения при x = b. Разделим отрезок [ x₀,b ] на п равных частей (полагаем, что b > x₀) и назовем шагом вычисления h длину отрезка [ x_i-1, x_i ]. Заменим на отрезке [ x₀, x₁ ] интегральную кривую отрезком ее касательной в точке (х₀, у₀). Ордината этого отрезка при х = х₁ равна y₁ = y₀ + hy₀΄, где у₀΄ = f(x₀,y₀). Так же найдем

y₂ = y₁ + hy₁΄, где y₁΄= f(x₁,y₁);

y₃ = y₂ + hy₂΄, где y₂΄= f(x₂,y₂);

..........................

y_n = y_n-1 + hy΄_n-1, где y΄_n-1 = f(x_n-1,y_n-1).

Можно предположить, что при 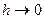построенные таким образом ломаные Эйлера приближаются к графику искомой кривой. Доказательство этого утверждения будет дано в следующей теореме:

Теорема 16.1 (теорема существования и единственности решения). Если в уравнении

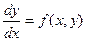
функция f(x,y) непрерывна в прямоугольнике D:

(16.5)

и удовлетворяет в D условию Липшица:

| f(x, y₁) – f(x, y₂) | ≤ N | y₁ – y₂ |, (16.6)

где N – постоянная, то существует единственное решение 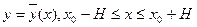,уравнения (16.2), удовлетворяющее условию (16.3), где

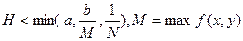в D.

Замечание 1. Нельзя утверждать, что искомое решение будет существовать при 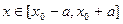, так как интегральная кривая может выйти из прямоугольника (16.5), и тогда решение может быть не определено.

Замечание 2. Условие Липшица (16.6) можно заменить более сильным требованием 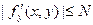в D. Тогда по теореме Лагранжа 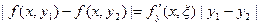, где 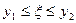. Таким образом, 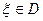и 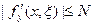. Поэтому .

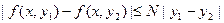Доказательство теоремы 16.1.

Заменим уравнение (16.2) с начальным условием (16.3) эквивалентным интегральным уравнением 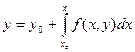. (16.7)

Легко проверить, что функция, обращающая в тождество уравнение (16.2), будет решением и уравнения (16.7).

Построим ломаную Эйлера у = у_п(х), исходящую из точки (х₀,у₀) с шагом на отрезке [ x₀, x₀ + H ] (аналогично можно доказать существование решения на [ x₀ – H, x₀ ]). Такая ломаная не может выйти за пределы D, так как угловые коэффициенты каждого ее звена по модулю меньше М. Теперь докажем последовательно три утверждения:

1) Последовательность у = у_п(х) равномерно сходится.

2) Функция 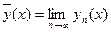является решением интегрального уравнения (16.7).

3) Решение 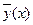уравнения (16.7) единственно.

Доказательство 1). По определению ломаной Эйлера

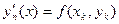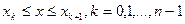при , или 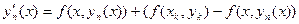. (16.8)

Обозначим 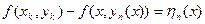, тогда в силу равномерной непрерывности f(x) в D 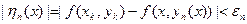(16.9)

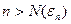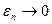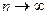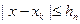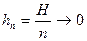при , где при , так как , а и при 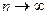. Интегрируя (16.8) по х в пределах от х₀ до х и учитывая, что 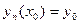, получим:

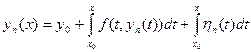. (16.10)

Так как п – любое целое положительное число, то для любого m > 0

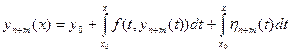, откуда

.

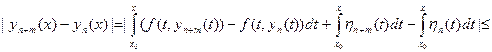
Тогда из (16.9) и условия Липшица следует, что

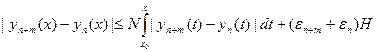. Следовательно,

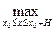
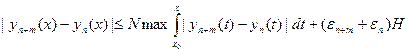, откуда

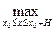
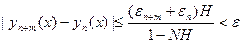
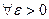при 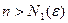, то есть последовательность непрерывных функций у_п(х) равномерно сходится при 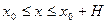к непрерывной функции 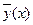. Итак, утверждение 1) доказано.

Доказательство 2). Перейдем в (16.10) к пределу при :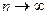

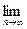
. (16.11)

В силу равномерной сходимости у_п(х) к 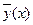и равномерной непрерывности f(x,y) в D последовательность f(x,y_n(x)) равномерно сходится к f(x, 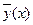). Действительно, 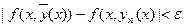при 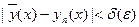, что выполняется при .

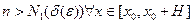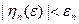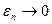Следовательно, возможен переход к пределу под знаком интеграла. Учитывая, что , где при 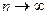, получим из (16.11):

,

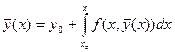то есть 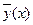удовлетворяет уравнению (16.7). Утверждение 2) доказано.

Доказательство 3). Предположим, что существуют два различных решения уравнения (16.7) у₁(х) и у₂(х), то есть 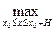| y₁(x) – y₂(x) | ≠ 0. Тогда, подставляя эти функции в (16.7) и вычитая полученные равенства друг из друга, получим:

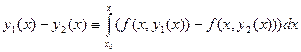, откуда

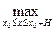| y₁(x) – y₂(x) | =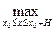

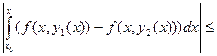
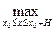
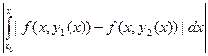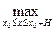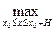
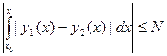
≤.Применим к этому неравенству условие Липшица: | y₁(x) – y₂(x) |≤ N 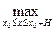| y₁(x) – y₂(x) |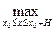

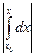
= NH 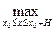| y₁(x) – y₂(x) |. Если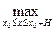| y₁(x) – y₂(x) | ≠ 0, то полученное равенство: 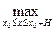| y₁(x) – y₂(x) | ≤ NH 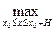| y₁(x) – y₂(x) | противоречиво, так как по условию теоремы 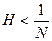. Следовательно, | y₁(x) – y₂(x) | = 0, то есть у₁(х) ≡ у₂(х).

Дата добавления: 2014-01-05