Прогнозирование ВР

Задача прогнозирования заключается в определении оценки следующего значения ВР при известных прошлых текущих значениях: y^{^}_t+i -?

Задача решается на основе модели тренда ВР.

Тренд – тенденция медленных и краткосрочных изменений ВР. Для описания тренда используют линейные либо линеарилзуемые функции. Предполагается, что функции локально адекватны (адекватно описывают ВР в окрестности y_t). Для определения параметров функции используют n значений ВР (текущее и n-1 - предыдущее). Здесь n – «основание прогноза» или длина обучающей выборки.

Для определения параметров используют МНК (или др.).

Поскольку характер тренда непрерывно меняется, используем адаптивные алгоритмы, в которых параметры определяются заново в каждый текущей момент времени.

Прогнозирующие функции делятся на:

1. полиномиальные, линейные относительно параметров:

y_t+i = b₀+ ∑ b_ji^j (8)

p- порядок модели, обычно 1 или 2; i – интервал прогнозирования.

zB1 Модель первого порядка (линейная):

y_t+i = b₀+ b₁i (9)

МНК- оценки коэффициентов:

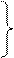b₀=2/(n(n+1))[(2n-1) ∑ y_t-i -3 ∑ i y_t-i ]

b₁=6/(n(n+1))[ ∑ y_t-i -2/(n-1) ∑ i y_t-i ] (10)

Модель второго порядка (квадратичная):

y_t+i = b₀+ b₁i + b₂i² (11)

МНК- оценки коэффициентов:

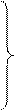b₀=3/(n(n+1)(n+2))[(3n(n-1)+2) ∑ y_t-i - 6/(2n-1) ∑ i y_t-i + 10∑ i² y_t-i ]

b₁=6/(n(n+1)(n+2))[3(2n-1) ∑ y_t-i - (2(2n-1)(8n-11))/((n-1)(n-2)) ∑ i y_t-i + 30/(n-2)∑ i² y_t-i ]

b₂=30/(n(n+1)(n+2))[ ∑ y_t-i - 6/(n-2) ∑ i y_t-i + 6/((n-1)(n-2)) ∑ i² y_t-i ]

(12)

1. Модели, сводящиеся к линейным:

а) степенная функция

y_t+i = ai^b (13)

может быть сведена к линейной (Y = lny; I = lni).

1. Экспоненциальные модели:

а) простая ЭМ:

y_t+i = ae^bi (→Y=lny) (14)

б) логарифмическая парабола:

y_t+i = ae^bi+ci2 (Y=lny) (15)

в) S-образная кривая:

y_t+i = e^a+b/i (Y=lny; I=1/i) (16)

4. Гиперболические модели:

а) первого типа:

y_t+i = a+b/i (I=1/i) (17)

б) второго типа:

y_t+i = 1/(a+b_i) (y=1/y) (18)

в) третьего типа:

y_t+i = i/(a+b_i) (y=1/y; I=1/i) (19)

5. Логарифмические модели:

а) логическая кривая:

y_t+i = a+blni (I=lni) (20)

б) обратнологарифмическая кривая:

y_t+i = 1/(a+blni) (y=1/y; I=lni) (21)

Параметры линеаризуемых функций находят обычно по МНК.

6. Модифицированная экспонента и сводящиеся к ней кривые:

а) модифицированная экспонента:

y_t+i = a+beⁱ (22)

(a,b,c. определяются по методу Брианта→(24))

б) кривая Гомперца:

y_t+i = ab^ei (Y=lny; A=lna; B=lnb) (23)

в) логистическая кривая Перла-Рида

y_t+i = 1/(a+beⁱ) (y=1/y; I=lni)

Метод Брианта:

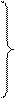с = ((n-1) ∑ y_t-iy_t-1-i - ∑ y_t-i ∑ y_t-1-i) / ((n-1) ∑ y²_t-i – [ ∑ y_t-i]²

b=(n- ∑ y_t-i cⁱ - ∑ y_t-i ∑ cⁱ) / (n ∑ c²ⁱ – [∑ c²ⁱ]²) (24)

a=(∑ y_t-i - b ∑ cⁱ) / n

7. Авторегрессионные модели:

y_t= - ∑ a_iy_t-i + u_t (25)

p-порядок; u_t-WN, возбуждающий модель АР; а_i- коэффициенты АР, определяемые из суммы уравнений Юла-Уолкера ((17)(31)).

zB_i для AP коэффициенты равны:

a₁= - (R_y(1)[R_y(0)-R_y(2)])/(R_y²(0)-R_y²(1)); a₂= - (R_y²(0)R_y(2)-R_y²(1))/ (R_y²(0)-R_y²(1)) (26)

Дата добавления: 2014-01-05