Обратимая реакция второго порядка

А D В.

ОБРАТИМАЯ РЕАКЦИЯ ПЕРВОГО ПОРЯДКА

В общем случае стехиометрическое уравнение обратимой реакции первого порядка имеет вид

Реакция одновременно протекает в двух противоположных направлениях, поэтому скорость такой реакции равна разности скоростей прямой и обратной реакций, каждая из которых является реакцией первого порядка, т.е. -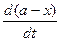 = k₁(a - x) – k₂(b + x),

где a и b — соответственно исходное количество вещества А и В, моль; x — количество вещества А, прореагировавшее к моменту времени t, моль.

Это следует из принципа независимости (принципа сосуществования) прямой и обратной реакций. Согласно этому принципу, если в системе одновременно протекает несколько реакций, то каждая из них независима от остальных и скорость ее прямо пропорциональна концентрациям реагирующих веществ. Конечное изменение концентрации данного вещества является результатом всех независимых изменений.

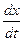= k₁(a - x) – k₂(b + x).

После преобразования уравнения будем иметь

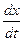= (k₁ + k₂)(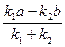- x).

Пусть

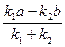= L,

тогда выражение примет вид

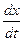= (k₁ + k₂)(L – x).

Разделив переменные, получим

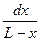= (k₁ + k₂)dt.

Проинтегрировав это выражение в пределах, соответственно от 0 до х и от 0 до t, и, решив его относительно k₁ +k₂, получим

k₁ + k₂ = ln.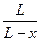

Следовательно, для нахождения суммы констант скоростей прямой и обратной реакций надо знать величину L, которую можно найти, разделив числитель и знаменатель в уравнении на k₂ и приняв во внимание, что

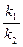= K,

где K — константа равновесия. В результате получим

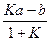= L.

Следовательно, для нахождения величины L необходимо знать константу равновесия данной реакции. Скорости прямой и обратной реакций в момент равновесия одинаковы, поэтому

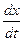= 0.

Oтметив количество вещества А, прореагировавшее к моменту равновесия, индексом ¥, получим

k₁(a - x_¥) – k₂(b + x_¥) = 0.

Отсюда

K = = .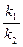

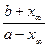Зная числовое значение L, можно рассчитать сумму констант скоростей k₁ + k₂,кроме того, зная числовое значение константы равновесия и учитывая, что она равна отношению констант скоростей прямой и обратной реакций, можно рассчитать каждую константу скорости в отдельности.

Иногда обратимую реакцию первого порядка формально удобно рассматривать как необратимую. Для этого можно считать, что к концу реакции прореагирует x_¥ исходного вещества. Тогда дифференциальное уравнение скорости реакции будет иметь вид

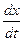= k(x_¥ - x).

Разделив переменные и проинтегрировав соответственно в пределах от 0 до х и от 0 до t, получим

k = ln.

Как видно из уравнений,

L = x_¥;

k = k₁ + k₂.

В общем виде эту реакцию можно записать так:

А + В D C + D.

Так же, как в предыдущем случае, скорость реакции будет равна разности скоростей прямой и обратной реакций, т. е.

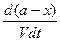- = k`<sub>1</sub>C<sub>A</sub>C<sub>B</sub> – k`₂C_CC_D,

где а—исходное число молей вещества А; х—число молей вещества А, прореагировавших к моменту времени t; V — объем системы; k`<sub>1</sub> и k`₂ — константы скоростей прямой и обратной реакций; С—концентрация реагирующих веществ моменту времени t

После дифференцирования получаем

= k`<sub>1</sub>C<sub>A</sub>C<sub>B</sub> – k`₂C_CC_D.

Рассмотрим наиболее простой случай, когда числа молей исходных веществ в начальный момент времени t = 0 одинаковы и равны величине а, а количества молей конечных веществ равны нулю. Тогда выражение примет вид

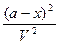= k`<sub>1</sub>- k`₂.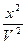

Сократив обе части уравнения на величину V, получим

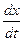= k₁(a – x)² – k₂x²,

где k₁ =; k₂ =.

В результате алгебраических преобразований будем иметь

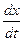= (k₁ – k₂)(x² - 2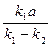x + ).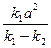

Выражение в скобках можно представить как произведение двух двучленов. Тогда

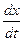= (k₁ – k₂)(m₁ – x)(m₂ – x),

где m₁ и m₂ — корни квадратного уравнения, которое можно записать так:

x² - 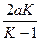x + = 0,

где K = k₁/k₂ — константа равновесия.

Корни уравнения равны

m_1,2 = .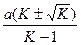

Разделив переменные в уравнении и проинтегрировав его, получим

k₁ – k₂ = ln.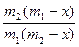

Зная константу равновесия K, можно найти константы скоростей прямой k₁ и обратной k₂ реакций.

Дата добавления: 2014-01-05