Параллельные реакции

Иногда исходные вещества реагируют одновременно в нескольких направлениях. Такие реакции называются параллельными. Рассмотрим простейший случай двух параллельных необратимых мономолекулярных реакций

A " B;

A " C.

Скорость первой реакции

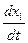= k₁(a – x);

второй

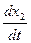= k₂(a – x),

где х₁ и х₂ — соответственно число молей веществ В и С, образовавшихся к моменту времени t; x = x₁+x₂—общее число молей вещества А, прореагировавшее к моменту времени t; k₁и k₂ — константы скоростей первой и второй реакций.

Скорость превращения вещества А по двум направлениям будет равна сумме скоростей превращения по каждому из направлений, т. е.

+ = .

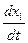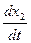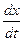Далее получим

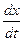= k₁(a – x) + k₂(a – x);

или

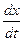= (k₁ + k₂)(a – x).

После интегрирования этого уравнения будем иметь

k₁ + k₂ = ln .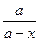

Это уравнение отличается от аналогичного уравнения для реакции первого порядка тем, что в уравнении стоит сумма констант скоростей обеих параллельных реакций. В случае трех параллельных реакций первого порядка в правой части уравнения будет стоять сумма трех констант.

Уравнение дает возможность определить сумму констант скоростей. Если же нужно найти каждую константу в отдельности, необходимо еще одно уравнение, в которое входили бы эти константы.

Разделив выражения, получим

= .

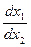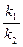После интегрирования этого уравнения в пределах соответственно от 0 до х₁ и от 0 до х₂ будем иметь

= .

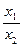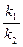Определив в некоторый момент времени количества веществ В и С, равные x₁ и x₂, получим отношение констант скоростей обеих параллельных реакций и, следовательно, решив совместно уравнения, получим возможность рассчитать каждую константу в отдельности.

Дата добавления: 2014-01-05