Примеры вычисления производных

Задание кривых и областей на комплексной плоскости.

Управление карьерой с позиций системного подхода.

Лекция 2. Карьерные цели и планирование карьеры.

Этические проблемы карьеры молодых специалистов.

Перед большинством современных работников необходимость соблюдения этических правил возникает, когда они сталкиваются с какой-то новой проблемой, решение которой основано на применении понятий «хорошо» и «плохо». Рассмотрим несколько подобных ситуаций.

Этика как экономический личностный интерес.

Рассмотрим ситуацию. Молодой специалист, работающий в фирме, получил предложение занять более высокую должность в конкурирующей компании. Его работодатель сделал попытку сохранить его на занимаемой должности. Беседуя с этим специалистом, его начальник сделал упор на морально-этические аспекты этой проблемы: надо уважать интересы фирмы, где его поставили на ноги, несмотря на связанные с этим затраты. Ответ молодого человека был: «Лояльность и этика имеют свою цену, и, как я полагаю, новый руководитель заплатит мне эту сумму».

Можно конечно критиковать этого молодого специалиста за избранный им лексикон и своеобразную этику, но он выразил сущность свободного рынка труда.

Согласно такой этике только соответствие требованиям нынешнего начальника создает для работника возможность поддерживать выгодную цену на свою индивидуальную работу.

Этика и законность.

Этика как правило принятого поведения.

Недопущение цинизма в суждениях.

Права и обязанности специалиста и его отношение к выполняемой работе.

На тип и характер карьерного процесса большое влияние оказывает то, как человек осуществляет свой выбор.

С точки зрения системного подхода под управлением следует понимать непрерывное целенаправленное воздействие субъекта управления на объект управления.

Изменение содержательности труда и повышение трудового потенциала работника могут быть достигнуты путем продвижения по ступенькам профессионально-квалификационной лестницы.

Так как 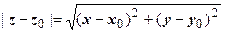равен расстоянию между точками z и z ₀, то

1. 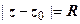- уравнение окружности радиуса R с центром в точке z ₀.

2. 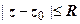- замкнутая область, ограниченная этой окружностью, т.е. круг радиуса R с центром в точке z ₀, включающий свою границу.

3. 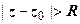- открытая область, состоящая из точек, находящихся вне круга радиуса R с центром в z ₀; круг не включен в эту область.

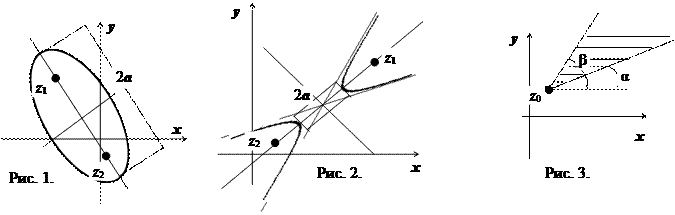
4. 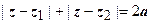- эллипс, построенный на точках z ₁ и z ₂, рассматриваемых как фокусы (большая полуось равна 2а, малая - 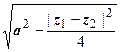) (рис. 1.). Области, лежащие внутри и вне эллипса, описываются соответствующими неравенствами.

5. 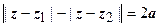- гипербола с фокусами в точках z ₁ и z ₂; расстояние между фокусами 2 с = 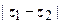, между вершинами 2 а (рис.2). Уравнение 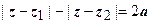даёт ветвь гиперболы, расположенную ближе к фокусу z ₂; неравенство 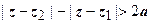- открытую область, содержащую фокус z ₁ и ограниченную соответствующей ветвью гиперболы.

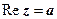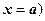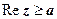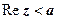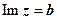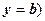6. (или - прямая, параллельная оси Оу. - область, лежащая справа от этой прямой (включая прямую); - область слева от прямой (прямая не включена в область). (или - прямая параллельная оси Ох; 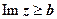, 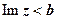- области, расположенные выше и ниже этой прямой.

7. 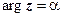- луч, выходящий из точки 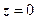под углом 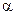к оси Ох. 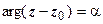- луч, выходящий из точки 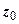под углом 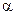к оси Ох. 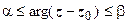- область, расположенная между лучами, выходящими из точки 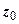(рис. 3.).

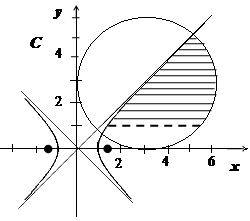
Пример построения области на комплексной плоскости, заданной системой неравенств:

построить область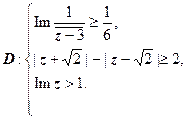

Определим, какая область даётся неравенством : ,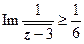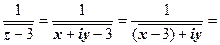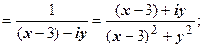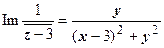

поэтому 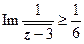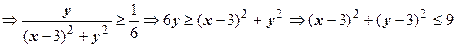- замкнутый круг радиуса 3 с центром в точке 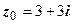. Неравенство 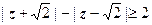даёт область, находящуюся справа от правой ветвью гиперболы с полюсами 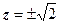, включающую эту ветвь. Параметры гиперболы: 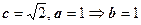. Последнее неравенство определяет полуплоскость 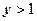. В результате получаем заштрихованную область, изображённую на рисунке справа.

19.1.6. Окрестности точек плоскости 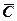. Под 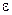- окрестностью точки 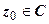понимается открытый круг радиуса 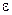с центром в точке 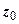: 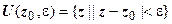. Проколотая окрестность точки 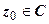- любая ее окрестность, из которой исключена сама точка 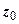: 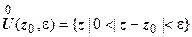. 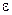- окрестность несобственной точки 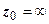- это внешность круга радиуса 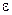с центром в начале координат (включающая саму точку 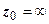): 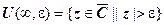. Проколотая 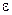- окрестность точки 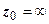- множество .

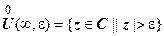19.2. Функция комплексной переменной.

19.2.1. Определение функции комплексной переменной ничем не отличается от общего определения функциональной зависимости. Напомним, что областью на плоскости мы называем любое открытое связное множество точек этой плоскости. Область односвязна, если любая подобласть, ограниченная непрерывной замкнутой самонепересекающейся кривой, лежащей в этой области, целиком принадлежит области.

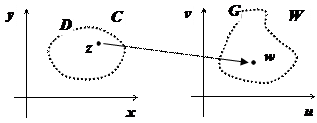
Рассмотрим две плоскости комплексных чисел: C = { z | z = x + iy } и W = { w | w = u + iv }. Пусть в плоскости С задана область D и задано правило, ставящее в соответствие каждой точке 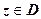определённое комплексное число 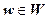. В этом случае говорят, что на области D определена однозначная функция w = f (z) (или определено отображение 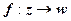). Область D называется областью определения функции, множество 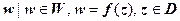- множеством значений функции (или образом области D при отображении f.

Если каждому 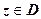ставится в соответствие несколько значений 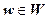(т.е. точка z имеет несколько образов), то функция w = f (z) называется многозначной.

Функция w = f (z) называется о днолистной в области 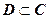, если она взаимно однозначно отображает область D на область 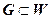(т.е. каждая точка 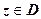имеет единственный образ 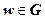, и обратно, каждая точка 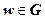имеет единственный прообраз .

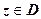19.2.2. Действительная и мнимая часть функции комплексной переменной. Так как

w = u + iv, z = x + iy, то зависимость w = f (z) можно записать в виде

w = u + iv = f (z) = f (x + iy) = Re f (x + iy) + i Im f (x + iy). Таким образом, задание комплекснозначной фу нкции w = f (z) комплексной переменной z равносильно заданию двух действительных функций u = u (x, y) = Re f (z), v = v (x, y) = Im f (z) двух действительных переменных х, у.

Примеры: 1. w = z ³. Выражаем z ³ через х, у: z ³ = (x + iy) ³ = x ³ + 3 x ² i y + 3 xi ² y ² + i ³ y ³ =

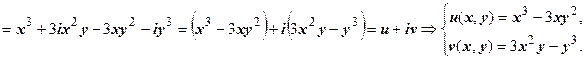
2. w = e ^z. Здесь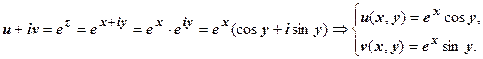

Дальше многие свойства ФКП (функций комплексной переменной) мы будем формулировать в терминах её действительной части u (x, y) и мнимой части v (x, y), поэтому техника выделения этих частей должна быть хорошо отработана.

19.2.3. Геометрическое изображнение ФКП. Задание функции w = f (z) как пары

u = u (x, y), v = v (x, y) наводит на мысль изображать ФКП как пару поверхностей u (x, y), v (x, y) в трёхмерном пространстве, однако этот способ неудобен, так как он не позволяет осмыслить пару (u, v) как комплексное число. Иногда изображают поверхность 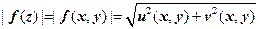, которую называют рельефом функции w = f (z). На эту поверхность наносят линии уровня функции Arg f (z); при наличии определенного опыта этой информации достаточно для того, чтобы составить представление об изменении функции в полярных координатах. Однако универсальный способ изображения ФКП состоит в том, что рисуют множества, соответствующие друг другу при рассматриваемом отображении. Чаще всего берут координатные линии (декартовых или полярных координат) и находят их образы.

Примеры. 1. Линейная функция w = a z + b, где 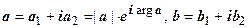- фиксированные комплексные числа, a ₁, b ₁ - их действительные части, a ₂, b ₂ - их мнимые части.

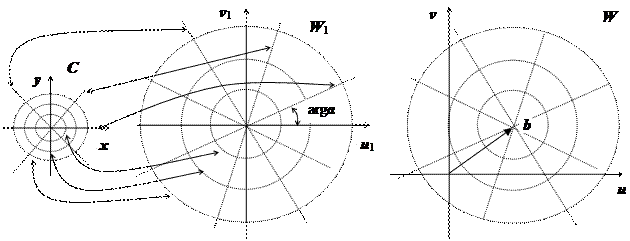
Представим эту функцию в виде суперпозиции двух функций: w ₁ = az и w = w ₁ + b. Отображение 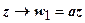, согласно интерпретации умножения чисел в тригонометрической форме, приводит к увеличению (уменьшению) аргумента числа z на arg a и растяжению (сжатию) его модуля в | a | раз; отображение 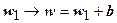приводит к сдвигу точки: w ₁ на вектор: b (b ₁, b ₂). Таким образом, линейная функция w = a z + b растягивает (при 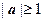) каждый вектор z в | a | раз (или сжимает его в 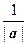раз при | a | <1), поворачивает на угол arg a и сдвигает на вектор b. В результате все прямые преобразуются в прямые, окружности - в окружности.

2. Степенная функция w = z ². Рассмотрим эту функцию в верхней полуплоскости

C ⁺ = { z | y = Im z >0}. В показательной форме w = z ² = (| z | e ^{i arg z})² = | z | ² e ^{2 i arg z}. Следовательно, полуокружность 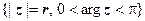переходит в окружность с выколотой точкой ,

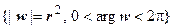луч 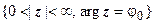- в луч 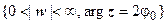. Вся верхняя полуплоскость С ⁺ перейдёт в плоскость W с выброшенной положительной полуосью.

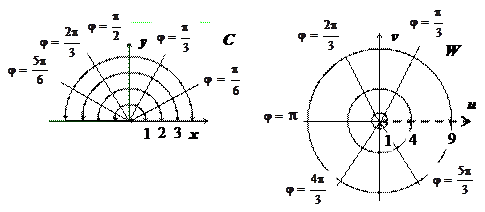Представим это отображение в декартовых координатах. Так как

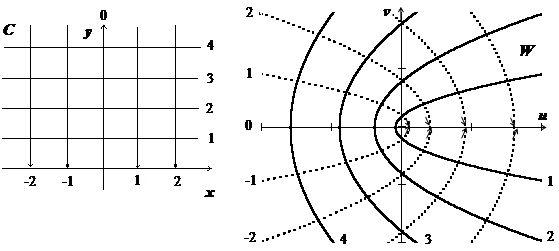w = z ² = (x + iy)² = x ² - y ² + 2 ixy, то u (x, y) = x ² - y ², v (x, y) = 2 xy. Найдём образы координатных линий. Прямая y = y ₀ перейдёт в кривую, параметрические уравнения которой u = x ² – y ₀²,

v = 2 xy ₀ (х - параметр). Исключая х, получим уравнение параболы 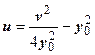. Луч 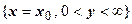перейдёт в u = x ₀² – y ²,

v = 2 x ₀ y (параметр y >0). Исключая у, получим ветвь параболы .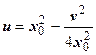

Из v = 2 x ₀ y следует, что v сохраняет знак x ₀, поэтому это будет верхняя ветвь при x ₀ >0, и нижняя при x ₀ <0. Луч x ₀ = 0 перейдет в луч u < 0, v = 0.

Мы рассматриваем функцию w = z ² в верхней полуплоскости С ⁺, несмотря на то, что она определена во всей плоскости С, по той причине, что она однолистна в этой полуплоскости. Нижняя полуплоскость C ^- = { z | y = Im z <0} при отображении w = z ² также накроет всю плоскость W (за исключением положительной полуоси). Если рассматривать весь образ плоскости С при этом отображении, то он будет состоять из двух экземпляров плоскости W (двух листов, накрывающих эту плоскость).

На этом примере мы получили алгоритм построения образов линий и областей при отображении w = f (z). Если w = u (x, y) + iv (x, y), то, чтобы найти уравнение образа линии L: F (x, y) = 0 при отображении, надо из системы уравнений 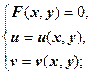исключить переменные х и у; в результате будет получено уравнение 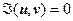образа линии L в плоскости W. Чтобы найти образ области D, ограниченной замкнутой кривой L, надо найти образ этой линии, если образ - замкнутая линия, дальше надо определить, переходит ли D в область, ограниченную этой линией, или во внешность этой области.

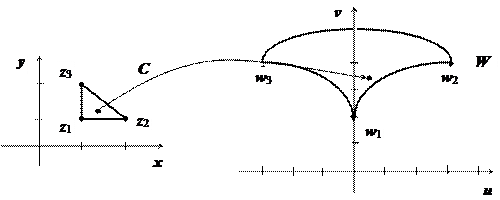Пример: пусть z ₁ = 1 + i, z ₂ = 2 + i, z ₃ = 1 + 2 i. Найти образ треугольника z ₁ z ₂ z ₃ при отображении w = z ².

Находим, куда отображаются вершины треугольника. w ₁ = z ₁² = (1 + i)² = 1 + 2 i - 1 = 2 i;

w ₂ = z ₂² = (2 + i)² = 4 + 4 i - 1 = 3 + 4 i;

w ₃ = z ₃² = (1 + 2 i)² = 1 + 4 i - 4 = -3 + 4 i. Сторона z ₁ z ₂ является частью прямой у = у ₀=1. Эта прямая отображается, как мы видели, в параболу 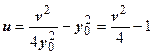. Нам нужна часть этой параболы между точками w ₁ и w ₂. Далее, сторона z ₁ z ₃ является частью прямой х = х ₀=1, отображаемой в параболу 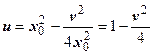; берём участок этой параболы между точками w ₁ и w ₃. Сторона z ₂ z ₃ лежит на прямой х + у =3; уравнение образа этой прямой получим, исключив из системы 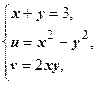переменные х и у: 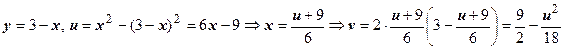. Участок этой параболы между точками w ₂ и w ₃ и даст образ стороны z ₂ z ₃. Изображение треугольника построено. Легко убедиться, что область, ограниченная этим треугольником, переходит во внутренность криволинейного треугольника w ₁ w ₂ w ₃ (для этого достаточно найти, например, образ одной точки этой области).

3. Более общая степенная функция w = z ⁿ, где n - натуральное число, действует аналогично функции w = z ². Так как w = zⁿ = (| z | e ^{i arg z}) ⁿ = | z | ⁿe ^{i n arg z}, то это отображение увеличивает в n раз все углы с вершиной в точке z = 0. Любые две точки z ₁ и z ₂ с одинаковыми модулями и аргументами, отличающимися на число, кратное 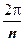(и только они), переходят в одну точку w, т.е. "склеиваются" при отображении. Следовательно, отображение неоднолистно ни в какой области, содержащей такие точки. Пример области, в которой это отображение однолистно - сектор 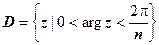. Этот сектор преобразуется в область 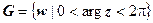, т.е. в плоскость W с выброшенной положительной полуосью. Любая область, заключенная в секторе раствора меньше 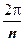, однолистно отображается в W.

19.2.4. Предел ФКП.

Определение. Пусть функция w = f (z) определена в проколотой окрестности точки z ₀ = x ₀ + iy ₀. Комплексное число w ₀ = u ₀ + iv ₀ называется пределом функции при 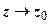, если для любой 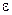-окрестности 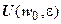(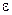>0) точки w ₀ найдётся такая проколотая 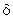-окрестность 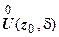точки z ₀, что для всех 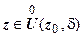значения f (z) принадлежат 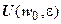. Другими словами, если z ₀ - собственная точка плоскости, то для любого 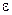>0 должно существовать такое 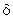>0, что из неравенства 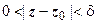следует неравенство 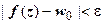(аналогично расписывается определение для несобственной точки 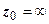). Таким образом, на языке 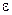-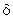определение предела ФКП полностью совпадает с определением предела функции одной действительной переменной; обозначается предел, как обычно: .

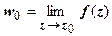Неравенство 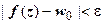означает, что 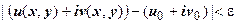, или 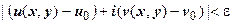. Для модуля комплексных чисел справедливы все основные свойства абсолютной величины, в частности 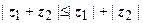, поэтому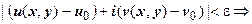 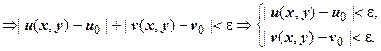Отсюда легко получить, что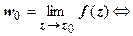 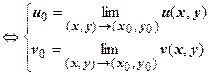. Таким образом, существование предела функции комплексной переменной равносильно существованию пределов двух действительных функций u (x, y) и v (x, y) двух действительных переменных. Поэтому в комплексный анализ автоматически переносятся все теоремы о пределах функции в точке (предел суммы функций и т.д.). Так же можно доказать, что если 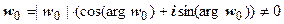, то (для существования нулевого предела достаточно, чтобы ).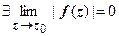

19.2.5. Непрерывность ФКП. Пусть функция w = f (z) определена в окрестности точки z ₀ = x ₀ + iy ₀. Функция называется непрерывной в точке z ₀, если:

1. существует ;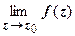

2. .

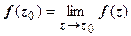Как и в случае предела, можно показать, что w = f (z) будет непрерывной в точке z ₀ = x ₀ + iy ₀ тогда и только тогда, когда функции u (x, y) и v (x, y) непрерывны в точке (x ₀, y ₀), поэтому на ФКП переносятся все основные теоремы о непрерывности функций.

19.3. Дифференцируемость функции комплексной переменной.

19.3.1. Определение производной. Аналитичность ФКП. Пусть w = f (z) определена, однозначна и принимает собственные значения в окрестности точки 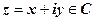. Производной функции w = f (z) в точке z называется предел 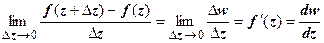. Функция, имеющая конечную производную в точке z, называется дифференцируемой в этой точке.

В этом определении важно, что стремление 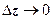может проходить по любому пути. Как мы увидим дальше, вследствие этого обстоятельства существование производной f’ (z) не сводится к существованию частных производных функций u (x, y) и v (x, y), а требует некоторых дополнительных условий. Сейчас мы дадим определение основного в теории ФКП понятия - аналитичности функции в точке и в области.

Определение. Однозначная функция называется аналитической (регулярной, голоморфной) в точке z, если она дифференцируема в некоторой окрестности этой точки.

Однозначная функция называется аналитической в области D, если она аналитична в каждой точке этой области.

Примеры. 1. f (z) = z ². В этом случае 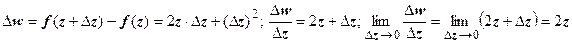. Таким образом, эта функция дифференцируема в любой точке, и её производная равна 2 z.

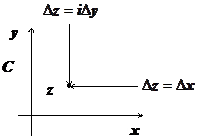2. f (z) = | z |² = x ² + y ². Докажем, что эта функция не имеет производной ни в какой точке 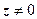. Будем стремить 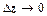по двум путям: по прямой, параллельной действительной оси Ох (в этом случае 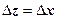), и по прямой, параллельной мнимой оси Оу (в этом случае 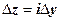). В первом случае 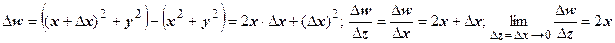, во втором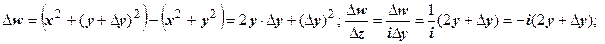 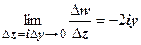. Эти пределы равны, только если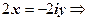 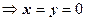. Таким образом, функция f (z) = | z |² = x ² + y ²может быть дифференцируема в единственной точке z = 0, во всех остальных точках пределы 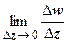различны в зависимости от способа стремления 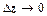, т.е. 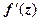не существует.

19.3.2. Условия Коши-Римана (Даламбера-Эйлера). Сейчас мы сформулируем и докажем важнейшую в теории ФКП теорему о необходимых и достаточных условиях дифференцируемости (а, следовательно, аналитичности) функции.

Для того, чтобы функция w = f (z) = u (x, y) + iv (x, y) была дифференцируема в точке z = x + iy, необходимо и достаточно, чтобы функции u (x, y) = Re f (z) и v (x, y) = Im f (z) были дифференцируемы в точке (х, у), и чтобы в этой точке выполнялись соотношения

.

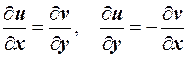Доказательство. Необходимость. Здесь мы применим идею, которой воспользовались, когда доказывали, что функция f (z) = | z |² = x ² + y ²не имеет производных в точках 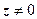: подойдём к точке z двумя путями - по направлениям 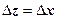(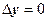) и ().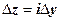

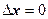В первом случае: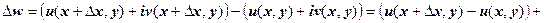

.

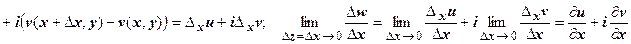Во втором случае: (напомню, что )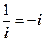

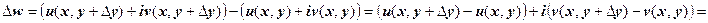
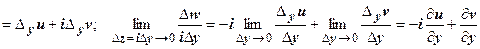. Пределы должны быть равны, поэтому .

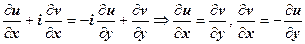Достаточность. По предположению теоремы, функции u (x, y), v (x, y) дифференцируемы в точке (х, у), поэтому 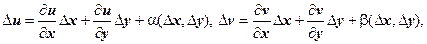где ,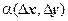

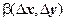- бесконечно малые более высокого порядка по сравнению с 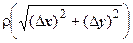, т.е. 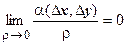, 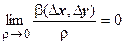. Найдём . .

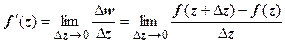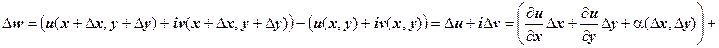
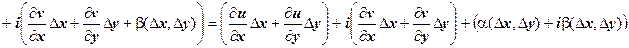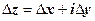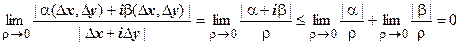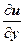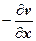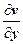Последнее слагаемое - бесконечно малая высшего порядка по сравнению с : ; далее, в предыдущих слагаемых, пользуясь формулами Коши-Римана, оставим только частные производные по х, т.е. заменим на , на 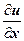; тогда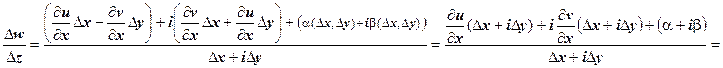 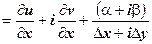. Отсюда следует, что существует 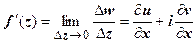, т.е. функция дифференцируема в точке (х, у).

Производная дифференцируемой функции может находиться по любой из формул 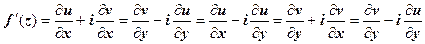, эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа: 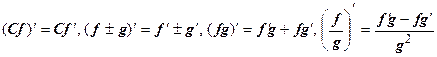(в точках, где .

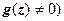1. Выше мы доказали, что функция f (z) = z ²имеет производную, равную 2 z, в каждой точке. Проверим, что для этой функции выполняются условия Коши-Римана. Так как

w = z ² = (x + iy)² = x ² - y ² + 2 ixy, то . Тогда .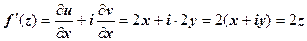

2. Для функции w = e ^z мы получили u (x, y) = e ^z cos y, v (x, y) = e ^z sin y. Поэтому 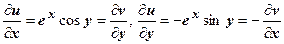, т.е. функция дифференцируема. .

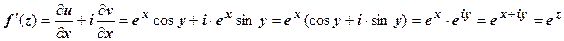19.3.4. Геометрический смысл производной. Равенство 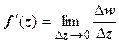означает, что 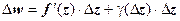, где 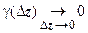. Отсюда, в частности, следует, что если функция дифференцируема в точке, то она непрерывна в этой точке. Будем писать 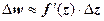, пренебрегая слагаемым высшего порядка малости. Пусть в точке z существует 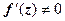. Возьмём точки z и 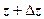; пусть w = f (z), тогда 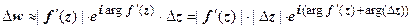. таким образом, 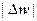в 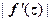больше 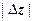, 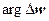больше 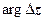на 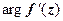для любого 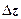(с точностью до бесконечно малых высшего порядка). Следовательно, в окрестности любой точки z, в которой 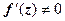, отображение 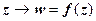действует следующим образом: любой вектор 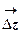растягивается в 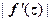раз и поворачивается на угол .

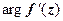Дата добавления: 2014-01-05