Конформность дифференцируемого отображения.

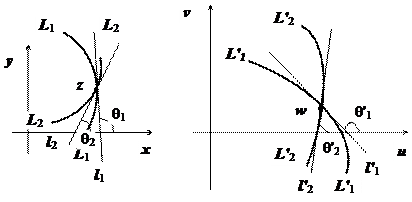
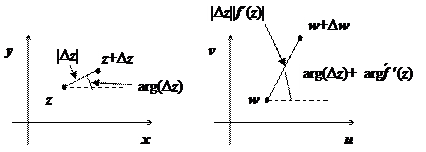Пусть через точку z проходят две гладкие кривые L ₁ и L ₂, касательные l ₁ и l ₂ к которым образуют с осью Ох углы, соответственно, 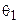и 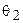. Образы этих кривых 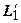и 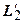при дифференцируемом отображении 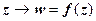имеют касательные 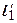и 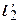, образующие с действительной осью Ou углы 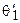и 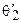. Согласно предыдущему пункту, , , 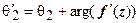т.е. 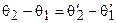. Таким образом, дифференцируемое отображение при 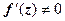сохраняет углы между кривыми. Сохраняется и направление отсчёта углов (т.е. если 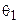>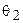, то >).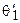

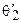Любое преобразование плоскости в плоскость, обладающее эти свойством (т.е. свойством сохранения углов), называется конформным. Если при этом сохраняется направление отсчёта углов, то преобразование называется конформным преобразованием первого рода; если направление отсчёта углов меняется на противоположное, то преобразование называется конформным преобразованием второго рода. Мы доказали, что аналитическая в некоторой области G функция w = f (z) осуществляет конформное отображение первого рода во всех точках, в которых производная отлична от нуля.

Пример конформного отображения второго рода – недифференцируемая функция .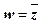

19.3.6. Гармоничность действительной и мнимой частей дифференцируемой функции. Дифференцируя первое соотношение Коши-Римана 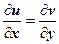по переменной х, второе соотношение 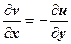по переменной у, получим 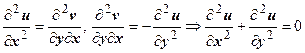, т.е. (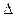- оператор Лапласа), т.е. u (x, y) - гармоническая функция. Дифференцируя первое соотношение Коши-Римана по переменной у, второе соотношение по переменной х, получим 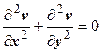, т.е. 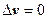, т.е. v (x, y) - тоже гармоническая функция. Пара гармонических функций, связанных соотношениями Коши-Римана, называется сопряжёнными функциями.

Легко доказать, что для любой гармонической в односвязной области D функции u (x, y) существует единственная (с точностью до постоянного слагаемого) сопряжённая с ней гармоническая функция v (x, y), т.е. такая функция, что w = f (z) = u (x, y) + iv (x, y) - аналитическая функция; и наоборот, для любой гармонической v (x, y) существует сопряжённая с ней гармоническая u (x, y). Пусть, например, дана u (x, y), обозначим 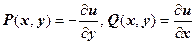. Эти функции удовлетворяют условию 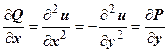, т.е. векторное поле 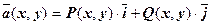потенциально. Функцию v (x, y) можно найти теперь из системы 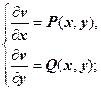(как это делается при решении уравнения в полных дифференциалах P (x, y) dx + Q (x, y) dy = 0, и как потенциальную для поля функцию .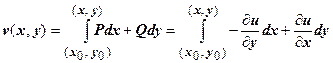

В качестве примера рассмотрим задачу, аналогичную задаче 5 из домашнего задания. Может ли функция v (x, y) = e ^{- y} (x cos x - y sin x) быть мнимой частью некоторой аналитической функции w = f (z)? В случае положительного ответа найти функцию w = f (z).

Решение. Докажем, что v (x, y) - гармоническая функция.

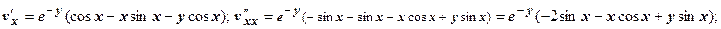
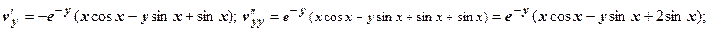
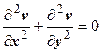, т.е. v (x, y) - гармоническая функция и, следовательно, может являться мнимой частью аналитической функции.

Найдём эту функцию. Для действительной части u (x, y) справедливы соотношения

,

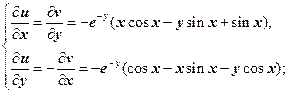
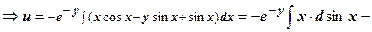
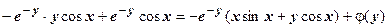для нахождения 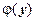используем второе уравнение системы: .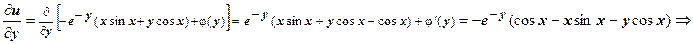

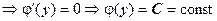Формально мы можем выписать

w = f (z) = u (x, y) + iv (x, y) = e ^{– y} [- (x sin x + y cos x) + i (x cos x - y sin x)] + C, но толку в этой записи нет, так как не видна зависимость f от z. Поэтому сделаем по-другому. Выпишем производную 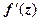: . На действительной оси (при у = 0, т.е при z = x) функция w = f (z) превращается в функцию действительной переменной f (x), её производная - в 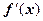. Положим в 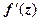у = 0, x = z: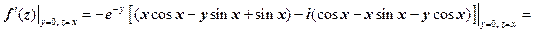 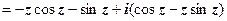; проинтегрировав это выражение, получим f (z).

Техника нахождения неопределённых интегралов в теории функций комплексной переменной в основном та же, что и в математическом анализе; таблица основных интегралов в обоих случаях одинакова, поскольку одинакова таблица производных. Поэтому

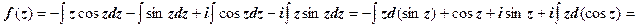
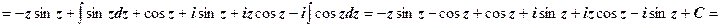= - z sin z + iz cos z + C = iz (cos z + i sin z) + C = ize^iz + C, где С – произвольная вещественная постоянная интегрирования. Постоянная интегрирования будет действительной, если по условию задачи задана функция v (x, y), и с точностью до произвольной постоянной находится действительная часть

u (x, y) функции f (z); если же задана функция u (x, y), то с точностью до произвольной постоянной интегрирования находится мнимая часть v (x, y), т.е постоянная будет чисто мнимым числом 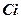(C - произвольное вещественное число).

Проверим полученный результат. Если f (z) = ize^iz + C, то f (z) = (ix - y) e ^{( ix - y )} + C =

= e ^{- y} (ix - y)(cos x + i sin x) + C = i e ^{- y} x cos x - e ^{- y} x sin x - e ^{- y} y cos x - i e ^{- y} y sin x + C = ;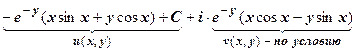

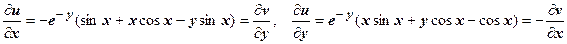; условия Коши-Римана выполнены, следовательно, функция f (z) = ize^iz + C - аналитическая на всей комплексной плоскости функция.

Во всех этих рассуждениях мы проигнорировали вопрос о том, имеют ли функции u и v производные порядка выше первого? (Существование первых производных следует, как мы видели, из дифференцируемости f (z)). Дальше мы докажем, что, в отличие от действительного случая, ФКП обладает удивительным свойством - если она аналитична в некоторой области (т.е. в каждой точке этой области имеет первую производную), то она бесконечно дифференцируема в этой области (т.е. в каждой точке этой области она имеет производную любого порядка). Как следствие, функции u и v тоже бесконечно дифференцируемы.

Дата добавления: 2014-01-05