Метод деления отрезка пополам (метод дихотомии, метод бисекции)

Основные этапы отыскания решения

В процессе приближенного отыскания корней уравнения (2.1) обычно выделяют два этапа: локализация (или отделение) корня и уточнение корня.

Локализация корня заключается в определении отрезка [ a, b ], содержащего один и только один корень. Не существует универсального алгоритма локализации корня. В некоторых случаях отрезок локализации может быть найден из физических соображений. Иногда удобно бывает локализовать корень с помощью построения графика или таблицы значений функции y = f (x). На наличие корня на отрезке [ a, b ] указывает различие знаков функции на концах отрезка. Основанием для этого служит следующая теорема математического анализа.

Теорема 2.1. Если функция f непрерывна на отрезке [ a, b ] и принимает на его концах значения разных знаков, так, что f (a) f (b) < 0, то отрезок [ a, b ] содержит по крайней мере один корень уравнения f (x) = 0.

Однако, корень четной кратности таким образом локализовать нельзя, так как в окрестности такого корня функция f (x) имеет постоянный знак.

На этапе уточнения корня вычисляют приближенное значение корня с заданной точностью e > 0. Приближенное значение корня уточняют с помощью различных итерационных методов. Суть этих методов состоит в последовательном вычислении значений x ₀, x ₁, …, x _n, …, которые являются приближениями к корню x ^*.

Метод деления отрезка пополам является самым простым и надежным способом решения нелинейного уравнения.

Пусть из предварительного анализа известно, что корень уравнения (2.1) находится на отрезке [ a ₀, b ₀], т. е. x 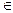^*[ a ₀, b ₀], так, что f (x ^*) = 0.

Пусть функция f (x) непрерывна на отрезке [ a ₀, b ₀] и принимает на концах отрезка значения разных знаков, т.е.

f (a ₀) f (b ₀) < 0. (2.2)

Разделим отрезок [ a ₀, b ₀] пополам. Получим точку x ₀ = . Вычислим значение функции в этой точке: f (x ₀). Если f (x ₀) = 0, то x ₀ – искомый корень, и задача решена. Если f (x ₀)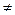0, то f (x ₀) – число определенного знака: f (x ₀) > 0, либо f (x ₀) < 0. Тогда либо на концах отрезка [ a ₀, x ₀], либо на концах отрезка [ x ₀, b ₀] значения функции f (x) имеют разные знаки. Обозначим такой отрезок [ a ₁, b ₁]. Очевидно, что x 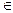^*[ a ₁, b ₁], и длина отрезка [ a ₁, b ₁] в два раза меньше, чем длина отрезка [ a ₀, b ₀]. Поступим аналогично с отрезком [ a ₁, b ₁]. В результате получим либо корень x ^*, либо новый отрезок [ a ₂, b ₂], и т.д. (рис. 2.2).

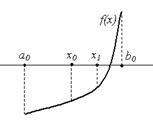
Рис. 2.2

Середина n-го отрезка x _n = 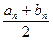. Очевидно, что длина отрезка [ a _n, b _n] будет равна 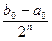, а т. к. x ^*[ a _n, b _n], то

| x _n – x 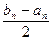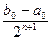^*| £ £ . (2.3)

Погрешность метода. Оценка (2.3) характеризует погрешность метода деления отрезка пополам и указывает на скорость сходимости: метод сходится со скоростью геометрической прогрессии, знаменатель которой q = 1/2. Заметим, что оценка (2.3) является априорной.

Критерий окончания. Из соотношения (2.3) следует, что при заданной точности приближения e вычисления заканчиваются, когда будет выполнено неравенство b _n – a _n < 2 e или неравенство n > log₂((b ₀ – a ₀)/ e) – 1. Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина x _n.

Пример 2.1.

Найдем приближенно x = 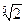с точностью = 0.01. Эта задача эквивалентна решению уравнения x ⁵ – 2 = 0, или нахождению нуля функции f (x) = x ⁵ – 2. В качестве начального отрезка [ a ₀, b ₀] возьмем отрезок [1, 2]. На концах этого отрезка функция принимает значения с разными знаками: f (1) < 0, f (2) > 0.

Найдем число n делений отрезка [1, 2], необходимых для достижения требуемой точности. Имеем:

| x _n – x 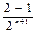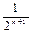^*| £ = £ 10^-2,

n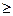6.

Следовательно, не позднее 6-го деления найдем 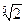с требуемой точностью, 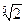» 1.1484. Результаты вычислений представлены в таблице 2.1.

Таблица 2.1

n	0 1 2 3 4 5 6
a n	1.0000 1.0000 1.0000 1.1250 1.1250 1.1406 1.1406
b n	2.0000 1.5000 1.2500 1.2500 1.1875 1.1875 1.1562
x n	1.5000 1.2500 1.1250 1.1875 1.1406 1.1562 1.1484
Зн f (a n)	- - - - - - -
Зн f (b n)	+ + + + + + +
f (x n)	5.5938 0.7585 -0.2959 0.1812 -0.0691 0.0532 -0.0078
b n – a n	1.0000 0.5000 0. 2500 0.1250 0.0625 0.0312 0.0156

Дата добавления: 2014-01-05