Метод простых итераций

Пусть уравнение (2.1) можно заменить эквивалентным ему уравнением

x = j (x). (2.4)

Например, уравнение – 0.5 = 0 можно заменить эквивалентным ему уравнением x = 0.5sin x.

Выберем каким-либо образом начальное приближение x ₀. Вычислим значение функции j (x) при x = x ₀ и найдем уточненное значение x ₁ = j (x ₀). Подставим теперь x ₁ в уравнение (2.4) и получим новое приближение x ₂ = j (x ₁) и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню:

x _n+1 = j (x_n). (2.5)

Формула (2.5) является расчетной формулой метода простых итераций.

Если последовательность { x _n} сходится при n®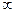, т. е. существует

x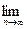^* = x_n, (2.6)

и функция j (x) непрерывна, то, переходя к пределу в (2.5) и учитывая (2.6), получим:

x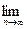^* = x_n = 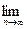j (x _{n - 1}) = j (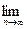x_{n - 1}) = j (x^*).

Таким образом, x ^* = j (x^*), следовательно, x ^* – корень уравнения (2.4).

Сходимость метода. Сходимость метода простых итераций устанавливает следующая теорема.

Теорема 2.2. Если в интервале, содержащем корень x^* уравнения (2.4), а также его последовательные приближения x ₀, x ₁, …, x _n, …, вычисляемые по формуле (2.5), выполнено условие:

| j' (x)| £ q < 1, (2.7)

то x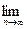^* =x_n.

т. е. итерационный процесс сходится и справедлива следующая оценка погрешности:

| x_n – x^* | £ qⁿ | x ₀ – x^* | (2.8)

Оценка (2.8) является априорной. Она показывает, что метод простой итерации сходится со скоростью геометрической прогрессии с знаменателем q. Чем меньше q, тем выше скорость сходимости.

Как следует из теоремы 2.2, условие (2.7) является достаточным для сходимости метода простых итераций. Его выполнение гарантирует сходимость процесса (2.5), но невыполнение условия (2.7), вообще говоря, не означает, что итерационный процесс будет расходиться.

На рис. 2.3 – 2.6 показаны четыре случая взаимного расположения линий y = x и y = j (x) и соответствующие итерационные процессы.

Рис. 2.3 и 2.4 соответствуют случаю | j' (x)| < 1, и итерационный процесс сходится. При этом, если j' (x) > 0 (рис. 2.3), сходимость носит односторонний характер, а если j' (x) < 0 (рис. 2.4), сходимость носит двусторонний, колебательный характер. Рис. 2.5 и 2.6 соответствуют случаю | j' (x)| > 1 – итерационный процесс расходится. При этом может быть односторонняя (рис. 2.5) и двусторонняя (рис 2.6) расходимость.

Рис. 2.3 Рис. 2.4 Рис. 2.5

Рис. 2.6

Погрешность метода. Если известна величина q в условии (2.7), то применима следующая апостериорная оценка погрешности:

| x_n – x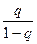^* | £ | x_n – x_{n – 1}|, n > 1. (2.9)

Критерий окончания. Из оценки (2.9) вытекает следующий критерий окончания итерационного процесса. Вычисления следует продолжать до выполнения неравенства

| x_n – x_{n – 1}| < e.

Если это условие выполнено, то можно считать, что x_n является приближением к x^* с точностью e.

Если q £ 0.5, то можно пользоваться более простым критерием окончания:

| x_n – x_{n – 1}| < e. (2.10)

Пример 2.2.

Используем метод простой итерации для решения уравнения f (x) = sin x – x ² = 0 с точностью e = 0.001.

Преобразуем уравнение к виду (2.4):

x = , т. е. j (x) = .

Нетрудно убедиться, что корень уравнения находится на отрезке [ p/6, p/ 3]. Например, вычислив значения f (x) на концах отрезка, получим: f (p / 6) > 0, а f (p /3) < 0, т. е. функция на концах отрезка имеет разные знаки, что в соответствии с теоремой 2.1 указывает на то, что внутри отрезка есть корень. Расположение корня наглядно иллюстрирует рис.2.7.

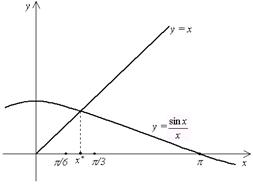
Рис. 2.7

Подсчитаем, первую и вторую производные функции j (x):

j '(x) = 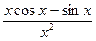, j "(x) = .

Так как j "(x) > 0 на отрезке [ p/6, p/ 3], то производная j '(x) монотонно возрастает на этом отрезке и принимает максимальное значение на правом конце отрезка, т. е. в точке p/ 3. Поэтому, справедлива оценка:

| j '(x)| £ | j '(p/ 3)|» 0.312.

Таким образом, условие (2.7) выполнено, q < 0.5, и можно воспользоваться критерием окончания вычислений в виде (2.10). В табл. 2.2 приведены приближения, полученные по расчетной формуле (2.5). В качестве начального приближения выбрано значение x ₀ = 1.

Таблица 2.2

n	xn
	0.8415 0.8861 0.8742 0.8774 0.8765

Критерий окончания выполняется при n = 5, | x₅ – x ₄| < 0.001. Сходимость двусторонняя, качественный характер такой сходимости представлен на рис. 2.4. Приближенное значение корня с требуемой точностью x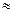^* 0.8765.

Дата добавления: 2014-01-05