
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интерполяция функции многочленами Лагранжа
|
|
|
|
Рассмотрим другой подход к приближению функции многочленами. Пусть функция y = f (x) определена на отрезке [ a, b ] и известны значения этой функции в некоторой системе узлов xi Î [ a, b ], i = 0, 1, …, n. Например, эти значения получены в эксперименте при наблюдении некоторой величины в определенных точках или в определенные моменты времени x 0, x 1, …, xn. Обозначим эти значения следующим образом: yi = f (xi), i = 0, 1, …, n. Требуется найти такой многочлен P (x) степени m,
P (x) = a 0 + a 1 x + a 2 x 2 + … + amxm, (4.5)
который бы в узлах xi, i = 0, 1, …, n принимал те же значения, что и исходная функция y = f (x), т. е.
P (xi) = yi, i = 0, 1, …, n. (4.6)
Многочлен (4.5), удовлетворяющий условию (4.6), называется интерполяционным многочленом.
Другими словами, ставится задача построения функции y = P (x), график которой проходит через заданные точки (xi, yi), i = 0, 1, …, n (рис. 4.1).
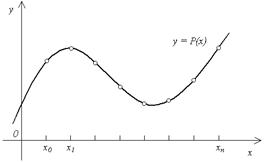
Рис. 4.1
Объединяя (4.5) и (4.6), получим:
a 0 + a 1 xi + a 2 x + … + amx
+ … + amx = yi, i = 0, 1, …, n. (4.7)
= yi, i = 0, 1, …, n. (4.7)
В искомом многочлене P (x) неизвестными являются m +1 коэффициент a 0 , a 1, a 2, …, am. Поэтому систему (4.7) можно рассматривать как систему из n +1 уравнений с m +1 неизвестными. Известно, что для существования единственного решения такой системы необходимо, чтобы выполнялось условие: m = n. Таким образом, систему (4.7) можно переписать в развернутом виде:
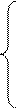 a 0 + a 1 x 0 + a 2 x
a 0 + a 1 x 0 + a 2 x + … + anx
+ … + anx = y 0
= y 0
a 0 + a 1 x 1 + a 2 x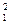 + … + anx
+ … + anx = y 1
= y 1
a 0 + a 1 x 2 + a 2 x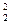 + … + anx
+ … + anx = y 2 (4.8)
= y 2 (4.8)
.
a 0 + a 1 xn + a 2 x + … + anx
+ … + anx = yn
= yn
Вопрос о существовании и единственности интерполяционного многочлена решает следующая теорема:
Теорема 4.1. Существует единственный интерполяционный многочлен степени n, удовлетворяющий условиям (4.6).
Имеются различные формы записи интерполяционного многочлена. Широко распространенной формой записи является многочлен Лагранжа
Ln (x) =  =
=  . (4.9)
. (4.9)
В частности, для линейной и квадратичной интерполяции по Лагранжу получим следующие интерполяционные многочлены:
L 1(x) = y 0 
 + y 1
+ y 1  ,
,
L 2(x) = y 0 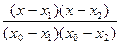 + y 1
+ y 1 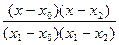 + y 2
+ y 2  .
.
Пример 4.3.
Построим интерполяционный многочлен Лагранжа по следующим данным:
| x | ||||
| y |
Степень многочлена Лагранжа для n +1 узла равна n. Для нашего примера многочлен Лагранжа имеет третью степень. В соответствии с (4.9)
L 3(x) = 1 +3
+3 + 2
+ 2 + 5
+ 5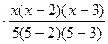 = 1 +
= 1 +  x –
x –  x 2 +
x 2 + 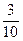 x 3.
x 3.
Пример 4.4.
Рассмотрим пример использования интерполяционного многочлена Лагранжа для вычисления значения заданной функции в промежуточной точке. Эта задача возникает, например, когда заданы табличные значения функции с крупным шагом, а требуется составить таблицу значений с маленьким шагом.
Для функции y = sinx известны следующие данные.
| x | p/6 | p/3 | p/2 | |
| y | ½ | 
|
Вычислим y (0.25).
Найдем многочлен Лагранжа третьей степени:
L 3(x) = 0 +
+ 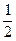
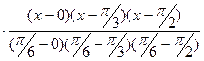 +
+

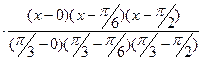 + 1
+ 1 .
.
При x = 0.25 получим y (0.25) = sin 0.25» 0.249.
Погрешность интерполяции. Пусть интерполяционный многочлен Лагранжа построен для известной функции f (x). Необходимо выяснить, насколько этот многочлен близок к функции в точках отрезка [ a, b ], отличных от узлов. Погрешность интерполяции равна | f (x) – Pn (x)|. Оценку погрешности можно получить на основании следующей теоремы.
Теорема 4.2. Пусть функция f (x) дифференцируема n + 1 раз на отрезке [ a, b ], содержащем узлы интерполяции xi Î [ a, b ], i = 0, 1, …, n. Тогда для погрешности интерполяции в точке x Î [ a, b ] справедлива оценка:
| f (x) – Ln (x)|£  | wn+ 1(x)|, (4.10)
| wn+ 1(x)|, (4.10)
где
Mn+ 1 =  | f ( n+ 1)(x)|,
| f ( n+ 1)(x)|,
wn+ 1(x) = (x – x 0)(x – x 1) …. (x – xn).
Для максимальной погрешности интерполяции на всем отрезке [ a, b ] справедлива оценка:
 | f (x) – Ln (x)| £
| f (x) – Ln (x)| £ 
 | wn (x)| (4.11)
| wn (x)| (4.11)
Пример 4.5.
Оценим погрешность приближения функции f (x) =  в точке x = 116 и на всем отрезке [ a, b ], где a = 100, b = 144, с помощью интерполяционного много члена Лагранжа L 2(x) второй степени, построенного с узлами x 0 = 100, x 2 = 144.
в точке x = 116 и на всем отрезке [ a, b ], где a = 100, b = 144, с помощью интерполяционного много члена Лагранжа L 2(x) второй степени, построенного с узлами x 0 = 100, x 2 = 144.
Найдем первую, вторую и третью производные функции f (x):
f '(x) = 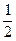 x – 1/2, f "(x) = –
x – 1/2, f "(x) = – x –3/2, f '''(x) =
x –3/2, f '''(x) =  x –5/2.
x –5/2.
M 3 =  | f '''(x)| =
| f '''(x)| =  100 –5/2 =
100 –5/2 =  10 –5.
10 –5.
В соответствии с (4.9) получим оценку погрешности в точке x = 116:
| – L 2(116)| £
– L 2(116)| £  |(116 – 100)(116 – 121)(116 – 144)| =
|(116 – 100)(116 – 121)(116 – 144)| = 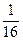 10 –5×16×5×28 = 1.4×10 – 3.
10 –5×16×5×28 = 1.4×10 – 3.
Оценим погрешность приближения функции f (x) =  на всем отрезке в соответствии с (4.11):
на всем отрезке в соответствии с (4.11):
 |
|  – L 2(x)| £
– L 2(x)| £ 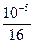
 |(x – 100)(x – 121)(x –144)|» 2.5×10–3.
|(x – 100)(x – 121)(x –144)|» 2.5×10–3.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 777; Нарушение авторских прав?; Мы поможем в написании вашей работы!