Постановка задачи численного интегрирования

Тема 5. Численное интегрирование функций одной переменной

Далеко не все интегралы можно вычислить по известной из математического анализа формуле Ньютона – Лейбница:

I = = F (b) – F (a), (5.1)

где F (x) – первообразная функции f (x). Например, в элементарных функциях не выражается интеграл 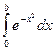. Но даже в тех случаях, когда удается выразить первообразную функцию F (x) через элементарные функции, она может оказаться очень сложной для вычислений. Кроме того, точное значение интеграла по формуле (5.1) нельзя получить, если функция f (x) задается таблицей. В этих случаях обращаются к методам численного интегрирования.

Суть численного интегрирования заключается в том, что подынтегральную функцию f (x) заменяют другой приближенной функцией, так, чтобы, во-первых, она была близка к f (x) и, во вторых, интеграл от нее легко вычислялся. Например, можно заменить подынтегральную функцию интерполяционным многочленом. Широко используют квадратурные формулы:

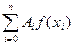» , (5.2)

где x_i – некоторые точки на отрезке [ a, b ],называемые узлами квадратурной формулы, A_i – числовые коэффициенты, называемые весами квадратурной формулы, n ³ 0 – целое число.

Дата добавления: 2014-01-05