Метод прямоугольников

Формулу прямоугольников можно получить из геометрической интерпретации интеграла. Будем интерпретировать интеграл как площадь криволинейной трапеции, ограниченной графиком функции y = f (x), осью абсцисс и прямыми x = a и x = b (рис. 5.1).

Рис. 5.1

Разобьем отрезок [ a, b ] на n равных частей длиной h, так, что h = 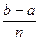. При этом получим точки a = x ₀ < x ₁ < x ₂ < … < x_n = b и x_{i+ 1} = x_i + h, i = 0, 1, …, n – 1 (рис. 5.2)

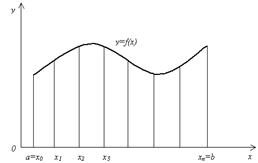
Рис. 5.2

Заменим приближенно площадь криволинейной трапеции площадью ступенчатой фигуры, изображенной на рис. 5.3.

Рис. 5.3

Эта фигура состоит из n прямоугольников. Основание i -го прямоугольника образует отрезок [ x_i, x_{i+ 1}] длины h, а высота основания равна значению функции в середине отрезка [ x_i, x_{i+ 1}], т е. f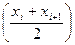 (рис. 5.4).

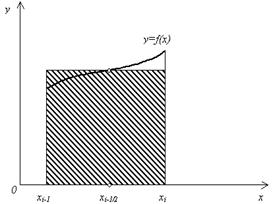
Рис. 5.4

Тогда получим квадратурную формулу средних прямоугольников:

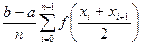I =» I _пр = (5.3)

Формулу (5.3) называют также формулой средних прямоугольников. Иногда используют формулы

I» I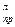 = 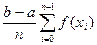, (5.4)

I» I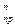 = 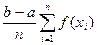, (5.5)

которые называют соответственно квадратурными формулами левых и правых прямоугольников.

Геометрические иллюстрации этих формул приведены на рис. 5.5 и 5.6.

Рис. 5.5

Рис. 5. 6

Оценка погрешности. Для оценки погрешности формулы прямоугольников воспользуемся следующей теоремой.

Теорема 5.1. Пусть функция f дважды непрерывно дифференцируема на отрезке [ a, b ]. Тогда для формулы прямоугольников справедлива следующая оценка погрешности:

| I – I _пр | £ h ², (5.6)

где M ₂ = | f "(x)|

Пример 5.1.

Вычислим значение интеграла 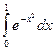по формуле средних прямоугольников (5.3) с шагом h = 0.1.

Составим таблицу значений функции e (табл. 5.1):

Таблица 5.1

x	e	x	e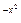
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50	1.0000000 0.9975031 0.9900498 0.9777512 0.9607894 0.9394131 0.9139312 0.8847059 0.8521438 0.8166865 0.7788008	0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00	0.7389685 0.6976763 0.6554063 0.6126264 0.5697828 0.5272924 0.4855369 0.4448581 0.4055545 0.3678794

Производя вычисления по формуле (5.3), получим:

I _пр = 0.74713088.

Оценим погрешность полученного значения. Имеем:

f "(x) = (e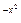)" = (4 x ² – 2) e.

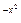Нетрудно убедиться, что | f "(x)| £ M ₂ = 2. Поэтому по формуле(5.4)

| I – I _пр | £ 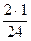(0.1)² » 0.84× 10^-3.

Дата добавления: 2014-01-05