Методика расчета средней арифметической величины по способу моментов

V, кг	Р	а	а • р
	2	+ 2	+ 4
		+ 1	+ 3
		- 1	- 6
		-2	- 8
		-3	- 3
n = 25	Sa • р = - 10 кг
i -интервал между группами = 1 кг

М_ср - рассчитанная при помощи метода моментов = 61,6 кг

Средняя арифметическая величина обладает тремя свой­ствами.

1. Средняя занимает серединное положение в вариационном ряду. В строго симметричном ряду: М = М₀=М_е.

2. Средняя является обобщающей величиной и за средней не видны случайные колебания, различия в индивидуальных данных, она вскрывает то типичное, что характерно для всей совокуп­ности. К средней обращаются всякий раз, когда надо исклю­чить случайное влияние от­дельных факторов, выявить об­щие черты, существующие за­кономерности, получить полное и глубокое представление о наиболее общих и характерных особенностях всей группы.

3. Сумма отклоне­ний всех вариант от средней равна нулю: S (V-M)= 0. Это происходит потому, что средняя величина превышает размеры одних вариант и мень­ше размеров других вариант.

Иначе говоря, истинное отклонение вариант от истинной средней (d = v-М) может быть положительной и отрицательной величи­ной, поэтому сумма S всех "+"d и "—"d равна нулю.

Данное свойство средней используется при проверке правильности расчетов М. Если сумма отклонений вариант от средней равна нулю, то можно сделать вывод, что средняя вычислена правильно. На этом свойстве основан способ моментов для определения М. Ведь если условная средняя А будет равна истинной М, то сумма отклонений вариант от условной средней будет равна нулю.

Роль средних величин в биологии чрезвычайно велика. С одной стороны их используют для характеристики явлений в целом, с другой - они необходимы для оценки отдельных величин. При сравнении отдельных величин со средними получают ценные харак­теристики для каждой из них. Использование средних величин требует строгого соблюдения принципа однородности совокупности. Нарушение этого принципа искажает представление о реальных процессах.

Вычисление средних из неоднородной в социально-экономическом отношении совокупности делает их фик­тивными, искаженными. Следовательно, для того чтобы правильно использовать средние величины, надо быть уверенным в том, что они характеризуют однородные статистические совокупности.

ХАРАКТЕРИСТИКА РАЗНООБРАЗИЯ ПРИЗНАКА В

СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ

Величина того или иного признака неодинакова у всех членов совокупности, несмотря на ее относительную однородность. Напри­мер, в группе детей, однородной по возрасту, полу и месту житель­ства, рост каждого ребенка отличается от роста сверстников. То же можно сказать о числе посещений, сделанных отдельными лицами в поликлинику, об уровне белка крови у каждого больного ревматизмом, об уровне артериального давления у отдельных лиц, больных гипертонической болезнью и т. п. В этом проявляется разнообразие, колеблемость признака в изучаемой совокупности. Вариабельность демонстративно можно представить на примере роста в группах подростков.

Статистика позволяет охарактеризовать это специальными крите­риями, определяющими уровень разнообразия каждого признака в той или иной группе. К таким критериям относятся лимит (lim), амплитуда ряда (Am), среднее квадратическое отклонение (s) и коффициент вариации (C_v). Так как каждый из этих крите­риев имеет свое самостоятельное значение, то следует остановиться на них отдельно.

Лимит - опреде­ляется крайними значе­ниями вариант в вариа­ционном ряду

Амплитуда (Am) - разность край­них вариант

Лимит и амплитуда - дают определен­ную информацию о степени разнообразия роста в каждой группе. Однако как лимит, так и амплитуда ряда обладает одним существенным недостатком. Они учитывают только разно­образие крайних вариант и не позволяют получить информацию о разнообразии признака в совокупности с учетом ее внутренней структуры. Дело в том, что разнообразие проявляется не столько в крайних вариантах, сколько при анализе всей внутренней структуры группы. Поэтому этими критериями можно пользоваться для при­ближенной характеристики разнообразия, особенно при малом чис­ле наблюдений (n<30).

Наиболее полную характеристику разноо­бразию признака в совокупности дает так называемое среднее квадратическое отклоне­ние, обозначаемое греческой буквой "сигма" - s.

Существует два способа расчета среднего квадратического отклонения: среднеарифметический и способ моментов.

При сред­неарифметическом способе расчета применяют формулу, где d - истинное отклонение вариант от истинной средней (V—M).

Формула используется при небольшом числе наблюдений (n<30), когда в вариационном ряду все частоты р= 1.

При р > 1 используют формулу такого вида:

При наличии вычислительной техники эту формулу приме­няют и при большом количестве наблюдений.

Эта формула предназначена для определения "сигмы" по способу моментов:

где: a - условное отклонение от условной средней (V-A); p -частота встречаемости для варианты; n - число вариант; i -величина интервала между группами.

Этот способ применяется в тех случаях, когда нет вычислитель­ной техники, а вариационный ряд громоздкий как за счет большого числа наблюдений, так и за счет вариант, выраженных многознач­ными числами. При числе наблюдений, равном 30 и менее, в момен­те второй степени п заменяют за (п —1).

Как видно из формулы среднего квадратичного отклонения (4), в знаменателе стоит (п —1), т.е. при числе наблюдений, равном или меньшем 30 (n£30), необходимо в знаменатель формулы брать (п —1). Если при определении средней арифметической М учиты­вают все элементы ряда, то, рассчитывая а, надо брать не все случаи, а на единицу меньше (п—1).

При большом числе наблюдений (n>30) в знаменатель формулы берут п, так как единица не изменяет результаты расчета и поэтому автоматически опускается.

Следует обратить внимание на то, что среднее квадратическое отклонение - именованная величина, поэтому оно должно иметь обозначение, общее для вариант и средней арифметической вели­чины (размерность – кг, см. км и др).

Расчет среднего квадратического отклонения по способу момен­тов производится после расчета средней величины.

Существует еще один критерий, характеризующий уровень раз­нообразия величин признака в совокупности, - коэффициент ва­риации.

Коэффициент вариации (Сv) - является относительной мерой разнообразия, так как исчисляется как процентное отноше­ние среднего квадратического отклонения (а) к средней арифме­тической величине (М). Формула коэффициента вариации такова:

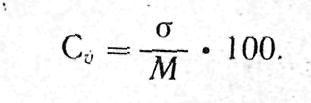
Для ориентировочной оценки степени разнообразия признака пользуются следующими градациями коэффициента вариации. Если коэффициент составляет более 20%, то отмечают сильное разно­образие; при 20—10% - среднее, и если коэффициент менее 10%, то считают, что разнообразие слабое.

Коэффициент вариации применяют при сравнении степени раз­нообразия признаков, имеющих различия в величине признаков или неодинаковую их размерность. Допустим, необходимо сравнить степень разнообразия массы тела у новорожденных и 5-летних детей. Понятно, что у новорожденных "сигма" всегда будет меньше, чем у семилетних детей, так как меньше их индивидуальная масса. Среднее квадратическое отклонение будет меньше там, где меньше величина самого признака. В этом случае для определения различия в степени разнообразия необходимо ориентироваться не на среднее квадратическое отклонение, а на относительную меру разнообразия - коэффициент вариации Сv.

Большое значение коэффициент вариации также имеет для оцен­ки и сопоставления степени разнообразия нескольких признаков с разной размерностью. По среднему квадратическому отклонению нельзя еще судить о различии в сте­пени разнообразия указанных признаков. Для этого необходимо использовать коэффициент вариации – Сv.

Среднее квадратическое отклонение связано со структурой ряда распределения признака. Схематич­но это можно изобразить следующим образом.

Теорией статистики доказано, что при нормальном распределе­нии в пределах М±s находится 68% всех случаев, в пределах М±2s - 95,5% всех случаев, а в пределах М±3s - 99,7% всех случаев, составляющих совокупность. Таким образом, М±3s охва­тывает почти весь вариационный ряд.

Это теоретическое положение статистики о закономерностях структуры ряда имеет огромное значение для практического при­менения среднего квадратического отклонения. Можно восполь­зоваться этим правилом для выяснения - вопроса о типичности средней величины. Если 95% всех вариант находятся в пределах М±2s, то средняя - является характерной для данного ряда и не требуется увеличивать число наблюдений в совокупности. Для опре­деления типичности средней сравнивается фактическое распреде­ление с теоретическим, путем расчета сигмальных отклонений.

Практическое значение среднего квадратического отклонения заключается также в том, что зная М и s, можно построить необходимые вариационные ряды для практического использования. Сигму (s) также используют для сравнения степени разнообразия однород­ных признаков, например при сравнении колебаний (вариабель­ности) роста детей в городе и селе местности. Зная сигму (s), можно рассчитать коэффициент вариации (Сv), необходимой для сравнения степени разнообразия признаков, выраженных в различных единицах измерения (сантиметрах, килограммах и др.). Это позволяет выявить более устойчивые (постоянные) и менее устойчивые признаки в совокупности.

Сравнивая коэффициенты вариации (C_v), можно сделать выводы о том, что является наиболее устойчивым признаком в совокупности признаков. Среднее квадратическое отклонение (s) используется также для оценки отдельных признаков у одного объекта. Стандартное отклонение указывает, на сколько сигм (s) от средней (М) отклоняются индивидуальные измерения.

Среднее квадратическое отклонение (s) может быть исполь­зовано в биологии и экологии при разработке проблем нормы и патологии.

Наконец, среднее квадратическое отклонение является важным компонентом формулы т_м — сред­ней ошибки средней арифметической (ошибки ре­презентативности):

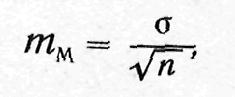
где т_м — средняя ошибка средней арифметической величины (ошибка репрезентативности), п — число наблюдений.

Репрезентативность. Важнейшие теоретические основы репрезентативности были освещены выше в разделе, посвященном выборочной и генеральной совокупности. Репрезентативность означает представительность в выборочной совокупности всех учитываемых признаков (пол, возраст, профессия, стаж и др.) единиц наблюдения, составляющих генеральную совокупность. Достигается эта репрезентативность выборочной совокупности по отношению к генеральной с помощью специальных методов отбора, которые излагаются ниже.

Оценка достоверности результатов исследования базируется на теоретических основах репрезентативности.

ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ

Под достоверностью статистических показа­телей следует понимать степень их соответствия отображаемой ими действительности. Достоверными результатами считаются те, которые не искажают и правильно отражают объективную реальность.

Оценить достоверность результатов исследования означает определить, с какой вероятностью возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность.

В большинстве исследований исследователю приходится, как правило, иметь дело с частью изучаемого явления, а выводы по результатам такого исследования переносить на все явление в целом - на генеральную совокупность.

Таким образом, оценка достоверности необходима для того, чтобы по части явления должно было бы судить о явлении в целом, о его закономерностях.

Оценка достоверности результатов исследования предусматривает определение:

1) ошибок репрезентативности (средних ошибок средних арифметических и относительных величин) - т;

2) доверительных границ средних (или относительных) величин;

3) достоверности разности средних (или относительных) величин
(по критерию t );

4) достоверности различия сравниваемых групп по критерию c ².

1. Определение средней ошибки средней (или относительной) величины (ошибки репре­зентативности) - т.

Ошибка репрезентативности (m) является важнейшей стати­стической величиной, необходимой для оценки достоверности ре­зультатов исследования. Эта ошибка возникает в тех случаях, когда требуется по части охарактеризовать явление в целом. Эти ошибки неизбежны. Они проистекают из сущности выбороч­ного исследования; генеральная совокупность может быть охарак­теризована по выборочной совокупности только с некоторой по­грешностью, измеряемой ошибкой репрезентативности.

Ошибки репрезентативности нельзя смешивать с обычным пред­ставлением об ошибках: методических, точности измерения, ариф­метических и др.

По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генераль­ной совокупности.

Этот единственный вид ошибок, учитываемых статистическими методами, которые не могут быть устранены, если не осуществлен переход на сплошное изучение. Ошибки репрезентативности можно свести к достаточно малой величине, т. е. к величине допустимой погрешности. Делается это путем привлечения в выборку достаточ­ного количества наблюдений (п).

Каждая средняя величина — М (средняя длительность лечения, средний рост, средняя масса тела, средний уровень белка крови и др.), а также каждая относительная величина — Р (уровень ле­тальности, заболеваемости и др.) должны быть представлены со своей средней ошибкой - т. Так, средняя арифметическая вели­чина выборочной совокупности (М) имеет ошибку репрезентатив­ности, которая называется средней ошибкой средней арифметической (m_м) и определяется по формуле:

Как видно из этой формулы, величина средней ошибки средней арифметической прямо пропорциональна степени разнообразия признака и обратно пропорциональна корню квадратному из числа наблюдений. Следовательно, уменьшение величины этой ошибки при определении степени разнообразия (s) возможно путем увели­чения числа наблюдений.

На этом принципе основан метод определения достаточного числа наблюдений для выборочного исследования.

Относительные величины (Р), полученные при выборочном исследовании, также имеют свою ошибку репрезентативности, которая называется средней ошибкой относительной величины и обозначается m_р

Для определения средней ошибки относительной величины (Р) используется следующая формула:

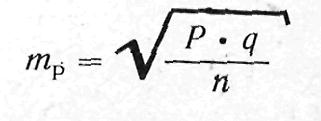
где Р — относительная величина. Если показатель выражен в про­центах, то q=100-P, если Р- в промиллях, то q=1000-P, если Р- в продецимиллях, то q= 10000- Р и т.д.; п — число наблю­дений. При числе наблюдений менее 30 в знаменатель следует взять (п – 1).

Каждая средняя арифметическая или относительная величина, полученная на выборочной совокупности, должна быть представ­лена со своей средней ошибкой. Это дает возможность' рассчи­тать доверительные границы средних и относительных величин, а также определить достоверность разности сравниваемых пока­зателей (результатов исследования).

Дата добавления: 2014-01-05