Определение доверительных границ М и Р

Определяя для средней арифметической (или относительной) величины два крайних значения: минимально возможное и мак­симально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами.

Доверительные границы — границы средних (или относительных) величин, выход за пределы кото­рых вследствие случайных колебаний имеет незна­чительную вероятность.

Доверительные границы средней арифметической в генеральной совокупности определяют по формуле:

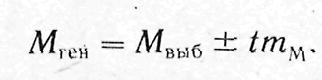
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:

где М _ген и Р_ген - значения средней и относительной величин, полученных для генеральной совокупности; М_выб и Р_выб - значения средней и относительной величин, полученных для выборочной совокупности; т _м и т_р — ошибки репрезентативности выборочных величин; t - доверительный критерий (критерий точности, который устанавливают при планировании исследования; t_m - доверитель­ный интервал; t_m =D, где D предельная ошибка показателя, полу­ченного при выборочном исследовании.

Размеры предельной ошибки (D) зависят от коэффи­циента t, который избирает сам исследователь, исходя из необхо­димости получить результат с определенной степенью точности.

Величина критерия t связана определенными отношениями с вероятностью безошибочного прогноза - р и численностью наблю­дений в выборочной совокупности. Они приведены в таблице.

Зависимость доверительного критерия / от степени вероятности безошибочного прогноза р (при n>30)

Степень вероятности безошибочного прогноза – P, %	Доверительный критерий t
95,0 % (0,05) 99,0 % (0,01)

Для большинства медико-биологических и социальный исследо­ваний достоверными считаются доверительные границы, установ­ленные с вероятностью безошибочного прогноза р = 95% и более. Чтобы найти критерий t при числе наблюдений п<30, необходимо воспользоваться специальной табл., в которой слева показано число наблюдений без единицы (n—1), а сверху (р) —степень вероятности безошибочного прогноза.

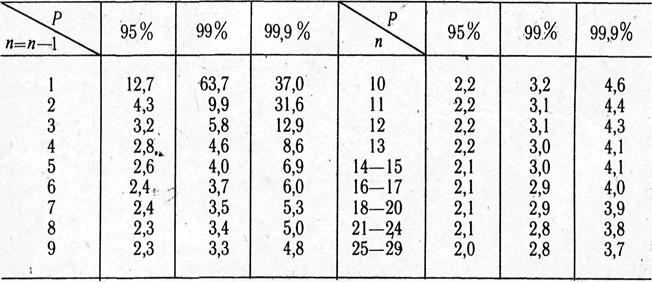
При определении доверительных границ сначала надо решить вопрос о том, с какой степенью вероятности безошибочного прогно­за необходимо представить доверительные границы средней или относительной величины. Избрав определенную степень вероятно­сти, соответственно этому находят величину доверительного крите­рия t при данном числе наблюдений. Таким образом, доверительный критерий t устанавливается заранее, при планировании исследо­вания.

Любой параметр (средняя величина или относительная величина) может оцениваться с учетом доверительных границ, полученных при расчете.

Как видно, доверительные границы зависят от размера дове­рительного интервала (t_m = D).

Анализ доверительных интервалов указывает, что при заданных степенях вероятности (р) и п >30 - t имеет неизменную величину и при этом доверительный интервал зависит от величины ошибки репрезентативности (m_м или т_р).

С уменьшением величины ошибки суживаются доверительные границы средних и относительных величин, полученных на выбо­рочной совокупности, т. е. уточняются результаты исследования, которые приближаются к соответствующим величинам генеральной совокупности.

Если ошибка большая, то получают для выборочной величины большие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности.

Доверительные границы М_выб и Р_вы6 зависят не только от средних ошибок этих величин (m_м или т_р), но и от избранной исследо­вателем степени вероятности безошибочного прогноза (р). При большой степени вероятности размах доверительных границ увели­чивается.

3. Определение достоверности разности средних (или относительных) величин (по критерию t). Критерий Стьюдента. В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т. д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их раз­ность, но и оценить ее достоверность.

Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.

Достоверность выборочной разности измеряется доверительным критерием (критерием точности t), который рассчитывается по специальным формулам для средних и относительных величин.

Формула оценки достоверности разности сравниваемых средних величин такова:

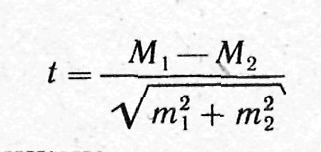
и для относительных величин:

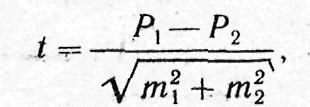
где М ₁, М ₂, Р₁,, P_{2 -} параметры, полученные при выборочных ис­следованиях; m₁ и m₂ - их средние ошибки; t - критерий точ­ности. Разность достоверна при t>2, что соответствует вероятности безошибочного прогноза, равной 95% и более (р>95,0%).

Для большинства исследований, проводимых в биологии, такая степень вероятности является вполне доста­точной.

При величине критерия достоверности t<2 степень вероятности безошибочного прогноза составляет <95%. При такой степени вероятности мы не можем утверждать, что полученная разность показателей достоверна с достаточной степенью вероятности. В этом случае необходимо получить дополнительные данные, увеличив число наблюдений.

Может случиться, что при увеличении численности выборки раз­ность продолжает оставаться недостоверной. Если при таких повторных исследованиях разность остается недостоверной, можно считать доказанным, что между сравниваемыми совокупностями не обнаружено различий по изучаемому признаку.

Указанная методика оценки достоверности и разности резуль­татов исследования позволяет проводить только попарное сравнение, групп при обязательном наличии обобщающих параметров - средних арифметических (М ₁ и М ₂) или относительных величин (Р₁ и P₂) и их средних ошибок (т).

Оценка достоверности различия сравниваемых групп по критерию" соответствия (хи-квадрат). Опре­деляя с помощью c² соответствие эмпирического распределения теоретическому, оценивают достоверность различия между выбороч­ными совокупностями.

Критерий c² (в отличие от критерия t) применяется в тех слу­чаях, когда нет необходимости знать величину того или иного параметра (среднюю или относительный показатель) и требуется оценить достоверность различия не только двух, но и большего чис­ла групп.

Так, критерий соответствия c² может быть использован для отве­та на следующие вопросы: существенно ли отличаются друг от дру­га группы вакцинированных и невакцинированных по распределе­нию их на больных и здоровых (т.е. эффективна ли вакцина); существенно ли отличаются группы населения с разным средне­душевым доходом по распределению их на больных и здоровых (т.е. влияет ли материальное обеспечение на уровень заболе­ваемости) и т. д.

Критерий c ² (хи-квадрат) определяется по формуле:

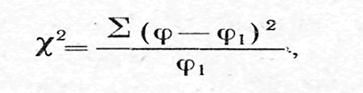
где ф - фактические (эмпирические) данные, ф1 – "ожидаемые" (теоретические) данные, вычисленные на основании нулевой гипо­тезы, å - знак суммы

"Нулевая гипотеза" - это предположение о том, что в сравниваемых группах отсутствует различие в распределении частот. Например, допускают одинаковое распределение больных и здоровых в группах вакцинированных и невакцинированных.

Определение критерия соответствия c² основано на расчете разницы между фактическими и «ожидаемыми» данными. Чем больше эта разность (ф - ф1), тем с большей вероятностью можно утверждать, что существуют различия в распределении сравнивае­мых выборочных совокупностей и, наоборот, чем меньше разность (ф - ф1), тем меньше шансов на то, что сравниваемые выборочные совокупности различны между собой.

Такой принцип доказательства "от противного" является до­вольно распространенным во многих исследованиях и применяется при расчете критерия c²

Последовательность расчета критерия на примере.

Требуется оценить при помощи критерия c² различаются ли по срокам заболеваемости корью группа вакцинированных и невакцинированных лиц (до вакцинации и после вакцинации).

Этапы расчета представлены в табл.

Таблица

Дата добавления: 2014-01-05