Лекция 3. Из физики известно, что эффективное рассеяние волн происходит, когда размер рассеивающих центров (дефектов) превышает четверть длины волны

Из физики известно, что эффективное рассеяние волн происходит, когда размер рассеивающих центров (дефектов) превышает четверть длины волны. В металлах энергия электронов проводимости сост. 3-15 эВ, это соотв. длине волны 3-7 А. Поэтому любые микронеоднородности структуры приводят к рассеянию электронов и росту уд. сопротивления материала.

В чистых металлах с совершенной структурой единственным фактором, ограничивающим длину свою пробега электронов, является тепловое колебание атомов в узлах решетки. С ростом температуры амплитуды колебаний увеличиваются, и поэтому растет удельное сопротивление.

Эти положения можно рассмотреть с помощью следующих выражений. Согласно классической теории Ме удельная проводимость может быть выражена:

,

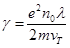где e – заряд электрона, n₀ – концентрация своб. электронов, λ – средняя длина своб. пробега электрона между двумя соударениями с узлами решетки, m – масса электрона, v_T – ср. скорость хаотического теплового движения своб-го электрона в металле. Из квантовой механики выводится , где К – числ. коэффициент.

Таким образом, n₀ и v_Т для разл. Ме при определенной температуре примерно одинаковы (число носителей заряда в том числе). Поэтому γ или ρ в основном зависят от длины св. пробега. Она же определяется структурой материала. Таким образом, тоже можно сделать вывод о том, что чем более правильная структура, тем меньше уд. сопротивление, а примеси, искажая решетку, приводят к увеличению ρ.

Зависимость ρ(Т)

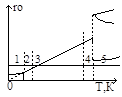
Это типичная кривая изменения уд. сопр. металлич. проводника от температуры. В узкой области 1 (несколько К) для ряда Ме может наступать состояние сверхпроводимости. При Т_св – скачок ρ. У чистых Ме сопротивление стремится к нулю при 0 К (пунктир). 2 – переходная область, где наблюдается быстрый рост уд. сопротивления ρ~Тⁿ(n может быть до 5 и снижается до 1 при Т=Θ_D)(температура Дебая определяет макс. частоту тепл. колебаний в кристалле :=hν_max/k – 400-450 К для больш. Ме.

Линейный участок 3 простирается почти до точки плавления (кроме ферромагнетиков, у которых есть еще доп. рассеяние из-за нарушений спинового порядка). 4 – может немного быть отступление от лин. зависимости, это начало плавления. При переходе из тв. в жидкое состояние у большинства Ме ρ увеличивается в 1.5-2 раза. Но могут быть и случаи со сложной крист. структурой (висмут, галлий), когда ρ уменьшается. При плавлении просто происходит разупорядочение, нарушение порядка расположения атомов.

Существует параметр, численно характеризующий зависимость ρ от температуры. Это температурный коэффициент удельного сопротивления. Он показывает относительное изменение уд-го сопротивления при изменении температруы на 1 Кельвин (⁰С):

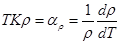
Положительный знак ТКρ означает, что с повышением Т в области данной точки ρ увеличивается. В области линейной зависимости ρ(Т) справедливо выражение:

Здесь ρ₀ и α₀ – соответствующие друг другу удельное сопротивление и ТКρ, отнесенные к началу температурного диапазона.

Большинство металлов имеют ТКρ~=0.0037 (К^-1).

Влияние дефектов на ρ. Мы уже говорили о том, что на ρ оказывают влияние тепловые колебания узлов решетки и статические дефекты структуры. Но в отличие от 1-го фактора, рассеяние электронов на статич. дефектах от температуры не зависит. Поэтому по мере приближения к абсолютному нулю сопротивление реальных металлов (т.е. с дефектами) стремится не к нулю, а к некоторому постоянному значению, которое называется остаточное сопротивление. Отсюда формулируется правило Маттиссена: удельное сопротивление металлов является аддитивной величиной, т.е. полное сопротивление металла есть сумма сопротивления, обусловленного рассеянием электронов на тепловых колебаниях узлов крист. решетки, и остаточного сопротивления, обусловленного рассеянием электронов на статических дефектах структуры.

Исключением правила Маттиссена являются сверхпроводящие металлы, в которых сопротивление исчезает ниже некоторой критической температуры.

Наиболее существенный вклад в ρ_ост вносят примеси (сущ-ют всегда): либо загрязнения, либо легирующие примеси (т.е. преднамеренно вводимые), причем любая примесная добавка приводит к увеличению ρ, даже материала с большей проводимостью. Примеси тем больше влияют на ρ, чем больше различаются валентности примесных атомов и металла-растворителя (основы).

Сюда еще можно добавить составляющую ρ_деф, возникающую из-за механич. деформаций (дислокаций, вакантных узлов или междоузельных атомов той же природы, что и осн. решетка, а также мех. напряжения, пластич. деформация).

Электрические свойства металлических сплавов. В технике широко применяются мет. сплавы, которые имеют структуру твердого раствора. Твердые растворы образуются из расплава при совместном отвердевании и кристаллизации металлов. Могут быть двух- и более компонентные сплавы. мы будем рассматривать примеры бинарных сплавов. Многие металлы с одинаковым типом крист. структуры образуют твердые растворы в любых пропорциях. Но существует также немало металлич. систем, компоненты которых обладают ограниченной взаимной растворимостью или не растворяются вообще.

Твердые растворы могут быть неупорядоченными. В этом случае сохраняется кристаллическая решетка металла-растворителя, изменяется только ее период. Атомы другого металла встраиваются в решетку и при этом располагаются статистически. Для такого сплавов сильное изменение периодичности поля решетки приводит к увеличению рассеяния электронов и, следовательно, к росту ρ.

где ρ_т – ρ, обусловленное рассеянием электронов на тепловых колебаниях решетки,

ρ_ост – ост. сопротивление, связанное в рассеянием электронов на неоднородностях структуры сплава.

Специфика твердых растворов состоит в том, что ρ_ост может существенно превышать ρ_т.

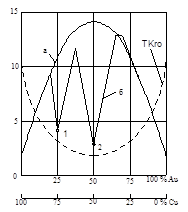
Есть закон Нордгейма:

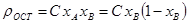, где С – константа, зависящая от природы сплава, x_A и x_B – атомные доли компонентов в сплаве.

По этому закону для двойных тв. растворов А-В ρ увеличивается как при добавлении А к В, так и В к А, т.е. безразлично, какой именно основной металл-растворитель. Это увеличение ρ симметрично относительно компонентного состава (см. рис., а). Остаточное ρ достигает максимума при содержании 50-50%. Закон не соблюдается, если наблюдаются фазовые переходы или элементы принадлежат к переходным или редкоземельным элементам.

Чем больше ρ сплавов, тем меньше его ТКρ. Это следует из того, что в тв. растворах ρ_ОСТ обычно существенно превышает ρ_Т и не зависит от температуры.

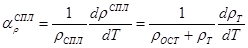
Так как ρ чистых металлов очень мало отличаются друг от друга, то

(*)

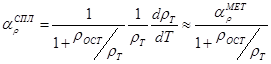Во многих случаях ТКρ сплавов значительно ниже ТКρ чистого металла и даже ниже значения, которое предсказывает формула (*). Может принимать также нулевое и отрицательные значения.

В физике выводится , где К – числ. коэффициент, n₀ – концентрация своб. электронов, λ – средняя длина своб. пробега электрона. Обычно n₀ в чистых металлах не зависит от температуры, и у них проводимость в основном определяется средней длиной свободного пробега электронов.

В сплавах же возможны ситуации, когда при повышении температуры частично возрастает концентрация носителей заряда. Сплав, у которого уменьшение длины своб. пробега компенсируется возрастанием концентрации носителей заряда, имеет ТКρ=0.

Это что касается неупорядоч. сплавов. Некоторые сплавы могут образовывать при определенных концентрациях компонентов упорядоченные сплавы, (см. рис., б). Например, Cu₃Au, CuAu. Упорядочение структуры происходит ниже некоторой критической температуры (т. Курнакова) (β-латунь: 50-50 медь и цинк - ОЦК). Выше этой т-ры атомы располагаются статистически.

Почему тут уменьшение ρ? Потому что при упорядочении восстанавливается периодичность расположения атомов и, следовательно, электростатического поля решетки, -> увеличивается λ и практически полностью исчезает добавочное сопротивление, обусловленное рассеянием на микронеоднородностях сплава.

Если компоненты сплава не растворяются друг в друге в твердом состоянии, то структура застывшего после кристаллизации сплава предст. смесь кристаллов каждого компонента. В этом случае удельное сопротивление изменяется линейно, т.е. возрастает пропорционально содержанию металла с бóльшим значением ρ.

Кратко рассмотрим другие св-ва.

Теплопроводность металлов. Тепло через металл передается теми же свободными электронами, которые определяют и электропроводность металлов. Поэтому коэффициент теплопроводности λ у металлов гораздо выше, чем у диэлектриков.

Чем больше удельная диэлектрическая проводимость γ металла, тем больше коэфф-нт его теплопроводности λ при прочих равных условиях. Закон, выражающий изменение взаимосвязи между λ и γ при изменении температуры наз-ся законом Видемана-Франца-Лоренца:

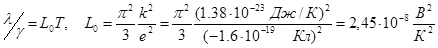
где Т – абс. температура, L₀ – число Лоренца, k – постоянная Больцмана.

Есть одно но: при низких температурах коэффициент L₀ уже не константа. Например, для Cu при уменьшении Т он проходит через минимум и при приближении к 0 К он снова ~ L₀.

Термоэдс. При соприкосновении двух различных металлов (или полупроводников) между ними возникает контактная разность потенциалов. Она обусловлена различием значений работы выхода электронов и различием значений концентрации свободных электронов соприкасающихся металлов. Термоэлемент, составленный из 2-х различных проводников, образующих замкнутую цепь, называют термопарой. Если спаи (контакты) находятся при разл. температурах, то в цепи возникает ток. Если цепь разорвать в произвольном месте, то на концах разомкнутой цепи появится разность потенциалов, кот. называется термоэдс. По имени первооткрывателя это явление наз-ся эффектом Зеебека. В небольшом температурном интервале термоэдс пропорциональна разности температур спаев:

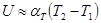
Коэфф-нт пропорциональности α_т – относительная дифференциальная или удельная термоэдс. Она зависит от природы соприкасающихся проводников и температуры. При комнатной температуре α_т ~ неск.мкВ/К. Существенно большее значение удельной термоэдс можно получить используя мет. сплавы со сложной зонной структурой.

Относительная удельная термоэдс α_т равна разности абсолютных удельных термоэдс составляющих проводников.

Металлические термопары используются для точного измерения температуры.

Сопротивление тонких металлических пленок. Размерные эффекты.

Металлические пленки широко используются в микроэлектронике в качестве обкладок конденсаторов, межэлементных соединений, контактных площадок, резистивных и магнитных элементов интегральных микросхем. Существует много методов получения тонких пленок, например, конденсация металлических паров в вакууме.

Электрические свойства тонких пленок металлов и сплавов значительно отличаются от свойств объемных образцов исходных проводниковых материалов. Одной из причин этого является то, что структура конденсируемых пленок при варьировании условий конденсации может очень сильно изменяться: от аморфной до полностью монокристаллической (эпитаксиальные пленки). Другая причина заключается в так наз. размерных эффектах. Это означает, что в тонких пленках возрастает роль поверхностных процессов по сравнению с объемными. Например, когда толщина пленки становится соизмерима со средней длиной свободного пробега электронов, уже нельзя допускать, что удельное сопр-е не зависит от геометрии образца.

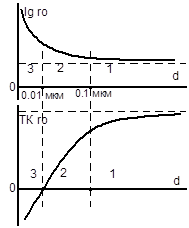
На различных стадиях конденсации структура пленок претерпевает существенные изменения. На рис. приведены типичные зависимости ρ и ТКρ от толщины пленки. Область 1) – ρ практически соответствует ρ массивного образца. 2) – ρ существенно больше ρ массивного образца, а ТКρ → 0. 3) – соответствует толщине ~10^-3 мкм, очень выс. ρ и отриц. ТКρ.

Чтобы это объяснить, надо принять во внимание, что пленки вначале имеют островковую структуру. На диэлектрической подложке вещ-во располагается в виде отдельных зерен-островков. Электропроводность пленки возникает еще до образования соединительных мостиков между островками при некотором минимальном количестве осажденного материала. Электроны могут переходить через узкие диэлектрические зазоры между островками – вследствие термоэлектронной эмиссии и туннелирования.

Сопротивление остр. мет. пленки во многом определяется поверхностным сопротивлением диэл. участков подложки, на кот. нет мет. зерен. Поверхн. сопротивление диэл. с повышением температуры падает, поэтому ТКρ отриц. При дальн. осаждении пленки зерна растут, зазоры уменьшаются, ТКρ по модулю становится меньше и при толщине ~ неск. нм меняется его знак на положительный. Далее островки сливаются, образуя проводящие цепочки, каналы, а затем и сплошной слой. На св-ва пленки большое влияние оказывают высокие концентрации дефектов – вакансий, дислокаций, границ зерен, и особенно примесных атомов, поглощенных из остаточных газов. Обычно окисляются границы зерен, и может расти отрицательный ТКρ.

Увеличению ρ пленки способствует и размерный эффект, т.е. сокращение длины свободного пробега электронов вследствие отражения от поверхности образца. Обычно поверхностное рассеяние играет значительную роль при норм. температуре, если толщина чистых мет. пленок меньше 200-300А. При низких температурах λ электронов возрастает, и разм. эффект сказывается при гораздо бóльших толщинах.

Для оценки проводящих свойств пленок пользуются параметром удельное поверхностное сопротивление. Тогда сопротивление тонкой мет. пленки рассчит-ся: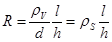

Уд. поверхностное сопотивление численно равно сопротивлению участка пленки, длина которого l равна его ширине h при прохождении тока через 2 его противоп.грани паралл-но пов-ти подложки. Т.е. уд. объемное сопр-е – это сопрот-е куба с единичной стороной., уд. поверхн. сопротивление – сопр-е квадрата любых размеров.

Делают тонкопленочные резисторы (в осн. тугопл. W, Mo, Ta, Cr) (R~500-1000 Ом/квадрат).

Дата добавления: 2014-01-05