Математическое ожидание и его свойства

Математическое ожидание (среднее значение) сл.в. 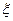является вероятностным обобщением понятия среднего арифметического.

Пусть некоторый опыт повторяется в неизменных условиях N раз, причем дискретная сл.в. приняла 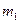раз знач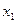ение , раз значение , …, раз значение :

.

Тогда среднее арифметическое 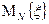результатов N измерений cл.в. 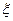равно

,

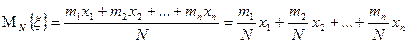где 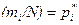- относительная частота появления значения 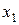, . При конечном N величина 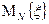изменяется от серии к серии, т.е. будет величиной случайной. Если , то в соответствии со статистическим определением вероятности относительные частоты перейдут в вероятности , а среднее арифметическое 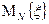- в м.о. :

.

Следовательно,

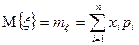, (2.8.1)

т.е. м.о. дискретной сл.в. равно сумме произведений возможных значений величины на их вероятности.

М.о. (средним значением) сл.в. 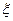называется значение, около которого группируются в опытах достаточно большой длины средние арифметические ее наблюдаемых значений.

М.о. 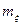больше наименьшего и меньше наибольшего возможных значений, т.е. на числовой оси возможные значения сл.в. расположены слева и справа от 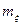. В этом смысле 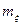. характеризует расположение распределения и поэтому его часто называют центром распределения сл.в. 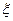. Это название связано с механической моделью сл.в.

Вероятностный смысл выражения состоит в том, что м.о. приближенно равно (и тем точнее, чем больше число опытов N) среднему арифметическому наблюдаемых значений сл.в. .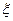

Когда n , то под м.о. понимают сумму соответствующего ряда. При этом должно удовлетворяться требование абсолютной сходимости ряда , т.е. должен сходиться ряд .

В ряде практических задач необходимо знать м.о. детерминированной функции от сл.в. , т.е. м.о. случайной величины . Например, требуется определить среднее значение энергии Е электрического сигнала по известным характеристикам амплитуды А (Е =).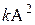

Функция случайного аргумента является также случайной, причем конкретное значение осуществляется тогда, когда сл.в. 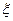принимает какое-либо конкретное значение . Так как функция детерминированная, то вероятность значения равна . Процесс образования функции случайного аргумента и вероятностей ее конкретных значений приведен в табл.2.1.

Таблица 2.1

			…
			…
			…

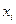
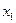
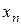
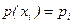
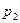
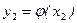
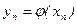
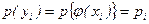
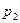
Последние две строки таблицы - не ряд распределения сл. в. , так как могут идти не в возрастающем порядке и, кроме того, некоторые значения могут совпадать. На основании формулы (1) и приведенной таблицы можно записать

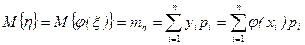. (2.8.2)

Формулы (1) и (2), справедливые для дискретной сл.в., обобщаются на непрерывные сл.в. Формула для м.о. непрерывной сл.в. имеет вид

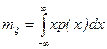. (2.8.3)

По аналогии можно получить формулу для м.о. функции сл.в.

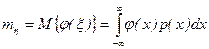. (2.8.4)

Из формулы (4) следует, что для определения м.о. любой функции сл.в. достаточно знать п.в. аргумента.

Размерность 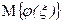совпадает с размерностью 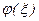. Отметим, что в математической литературе 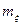обычно называют математическим ожиданием, а в технической - чаще всего средним значением сл.в. .

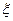Рассмотрим основные свойства математического ожидания.

1.М.о. сл.в. 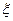есть некоторая постоянная (неслучайная) величина, имеющая размерность самой сл.в., т.е.

. (2.8.5)

2. М.о. постоянной величины С равно самой постоянной величине:

. (2.8.6)

В самом деле, .

3. Постоянный множитель С можно выносить за знак м.о.:

. (2.8.7)

Действительно,

.

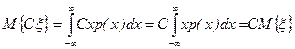4. М.о. суммы (разности) случайных величин 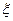и равно сумме (разности) их м.о., т.е.

. (2.8.8)

Докажем это утверждение

В частности, если 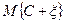, где С=const, то

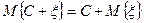. (2.8.9)

5. М.о. произведения независимых сл.в. 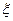и равно произведению их м.о.:

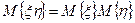. (2.8.10)

В самом деле,

.

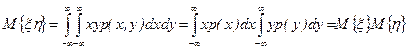6. Математическое ожидание сл.в. 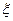, имеющей симметричную плотность вероятности относительно прямой 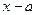, т.е. 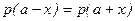, равно 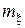= a. Это следует из очевидного равенства

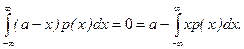
В дальнейшем часто придется иметь дело с центрированной сл.в. 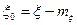, которая представляет собой разность между сл.в. 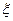и ее м.о. 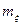, т.е. это такая величина, значения которой отсчитываются относительно м.о. Отметим два её свойства.

М.о. центрированной сл.в. равно нулю:

.

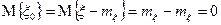Есл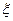и и независимы, то . Действительно,

. (2.8.11)

В качестве характеристик положения, кроме м.о. 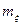, используются иногда мода и медиана .

Модой непрерывной сл.в. называется такое ее возможное значение, при котором п.в. p(x) имеет максимальное значение (рис.2.11)

.

Для дискретной сл.в. модой является такое , которое имеет наибольшую вероятность (рис.2.12).

Если распределение имеет более одного максимума, то оно называется многомодальным или полимодальным (рис.2.13 и рис.2.14). Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом. Такие распределения называются антимодальными (рис.2.15 и рис.2.16).

Пример 2.8.1. Случайная величина 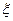задана распределением

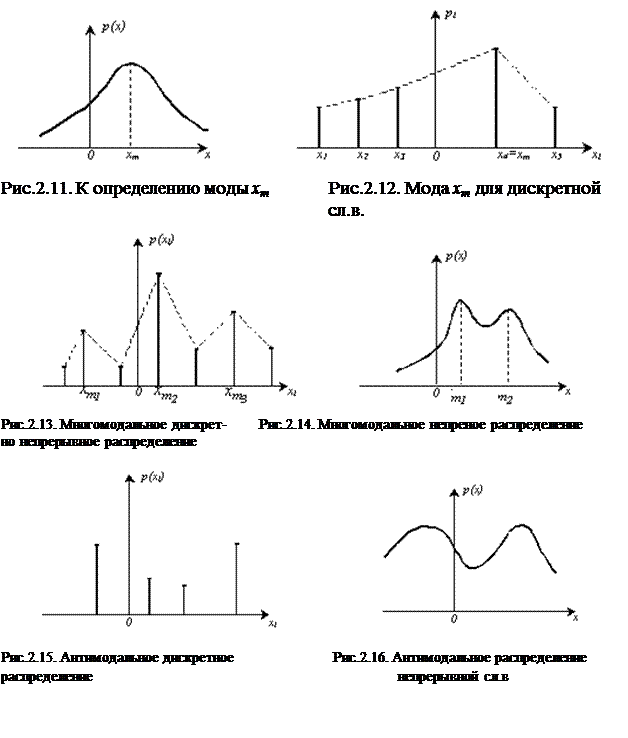
	-1
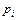
	0,2	0,3	0,5

Определить м.о. следующих сл.в. 1)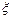, 2) , 3) .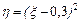

1) .

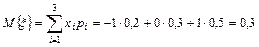2) Чтобы определить надо найти возможные значения сл.в. . При ; если 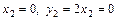; когда .

Закон распределения сл.в. будет иметь вид

	-2
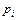
	0.2	0.3	0.5

, т.е. удвоение значений сл.в. приводит к удвоению ее м.о.

3) Для сл.в. 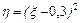ряд имеет вид

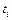
	1,69	0,09	0,49
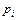
	0,2	0,3	0,5

Тогда

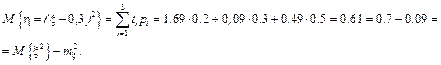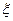Медианой сл.в. называется такое ее возможное значение x =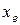, для которого . Геометрически медиана - это абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам (рис.2.17).

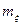Если пл.в. одномодальна и симметрична, то все ее характеристики положения (, , ) совпадают. Соотношения между м.о. 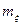, модой и медианой показаны на рис.2.18.

М.о. 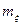”чувствительно” к “хвостам” закона распределения, медиана 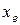менее чувствительна к ним, а на моду 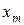крайние значения вообще не влияют. Для унимодального и симметричного з.р. все три показателя совпадают. Для асимметричных и мультимодальных распределений такого совпадения нет. П.в. имеет положительную (отрицательную) асимметрию, если мода предшествует медиане (следует за медианой). При этом большая часть распределения находится справа (слева), а более крутой спад - слева (справа) от моды.

Дата добавления: 2014-01-05