Загальна формула для обчислення похибки

Нехай потрібно обчислити значення функції

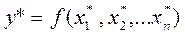при заданих значеннях незалежних змінних. Якщо при цьому замість точних значень 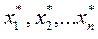, які нам не відомі, підставляються їх наближені значення 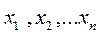(причому 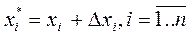), то при обчисленні значення функції виникає похибка

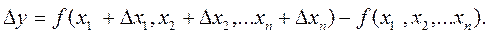
Припустивши, що функція 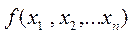диференційована (достатню кількість разів), Δ у можна подати у вигляді

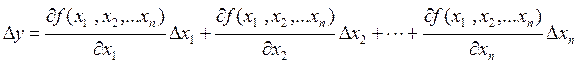(1.2) плюс члени другого і вищих порядків відносно Δ х_і..

Якщо похибки Δ х_і за абсолютною величиною досить малі, то членами другого і вищих порядків у виразі (1.2) можна знехтувати. Тоді для абсолютної похибки наближеного значення у матимемо:

,

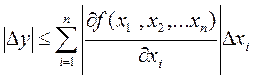де через Δ х_і позначені граничні абсолютні похибки аргументів. Таким чином,

. (1.3)

Для граничної відносної похибки δ_у маємо:

,

Або

(1.4)

З формули (1.3) випливає, що гранична абсолютна похибка суми наближених чисел а₁ + а₂ + ••• + а_п... дорівнює сумі їх граничних абсолютних похибок. Для різниці двох чисел а = а₁ — а₂ маємо: 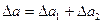. При цьому відносна похибка різниці може виявитись досить великою, якщо числа а₁ та а₂ між собою мало відрізняються і їх різниця близька до нуля. У цьому випадку для забезпечення потрібної точності треба мати в зменшуваному і від'ємнику достатню кількість цифр, щоб гранична абсолютна похибка різниці а була меншою від самої різниці. Тому по можливості слід уникати віднімання близьких чисел.

Для похибки добутку додатних чисел а = а₁а₂...а_п з (1.4) маємо:

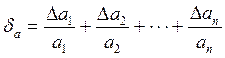
тобто гранична відносна похибка добутку кількох наближених додатних чисел, що відрізняються від нуля, дорівнює сумі граничних відносних похибок цих чисел.

Легко переконатись, що гранична відносна похибка частки дорівнює сумі граничних відносних похибок діленого і дільника.

Справді, нехай 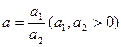. Тоді з (1.4) маємо:

.

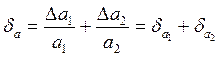Можна переконатися також, що відносна похибка к-го степеня числа а у к раз більша, ніж відносна похибка числа а. Аналогічно відносна похибка кореня к-го порядку з числа а у к раз менша, ніж відносна похибка числа а.

Дата добавления: 2014-01-05