
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные рпределения, координаты вектора
|
|
|
|
Декартова прямоугольная система координат в пространстве определяется заданием трех взаимно перпендикулярных осей с общим началом отсчета (начало координат) и одинаковой для всех осей масштабной единицей. (В дальнейшем будем называть ее просто прямоугольной или декартовой) (рис. 2.1). Оси носят название:
· 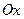 – ось абсцисс;
– ось абсцисс;
· 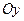 – ось ординат;
– ось ординат;
·  – ось аппликат.
– ось аппликат.
Плоскости xОy, xОz, yOz называются координатными плоскостями.
Единичные векторы 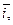
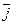 ,
, 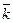 , сонаправленные с осями Ox, Oy, Oz, носят название: орт осей. Если орты образуют правую тройку, то система координат называется правой, если левую, то – левой. В дальнейшем мы будем работать только с правой системой координат (рис. 2.1).
, сонаправленные с осями Ox, Oy, Oz, носят название: орт осей. Если орты образуют правую тройку, то система координат называется правой, если левую, то – левой. В дальнейшем мы будем работать только с правой системой координат (рис. 2.1).
Определим понятие координат вектора. Рассмотрим произвольный вектор 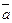 . Приведем его к началу координат, точке
. Приведем его к началу координат, точке 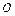 (рис. 2.1). (Напомним, мы рассматриваем только свободные векторы). Спроектируем этот вектор на координатные оси. Составляющими вектора
(рис. 2.1). (Напомним, мы рассматриваем только свободные векторы). Спроектируем этот вектор на координатные оси. Составляющими вектора 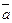 по координатным осям являются векторы:
по координатным осям являются векторы: 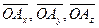 , а проекциями на координатные оси – числа
, а проекциями на координатные оси – числа 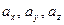 . Эти проекции мы и будем называть координатами вектора.
. Эти проекции мы и будем называть координатами вектора.
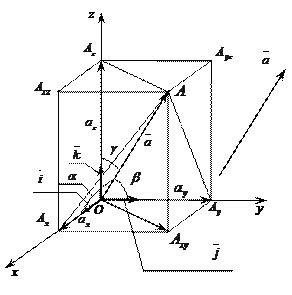
Рис. 2.1
Определение 2.1. Координатамивектора 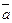 называются его проекции
называются его проекции 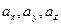 на координатные оси. При этом пишут:
на координатные оси. При этом пишут:
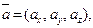 (2.1)
(2.1)
где 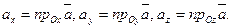 Очевидно, координаты нулевого вектора равны 0.
Очевидно, координаты нулевого вектора равны 0.
Если два вектора равны, 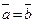 , то равны их проекции на оси, а значит и их координаты. И наоборот, если равны координаты двух векторов, то равны и векторы. Следовательно, справедливо утверждение.
, то равны их проекции на оси, а значит и их координаты. И наоборот, если равны координаты двух векторов, то равны и векторы. Следовательно, справедливо утверждение.
Теорема 2.1. Необходимым и достаточным условием равенства двух векторов является равенство их соответствующих координат:
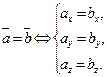 (2.2)
(2.2)
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 347; Нарушение авторских прав?; Мы поможем в написании вашей работы!