Плавание тел

Сила давления жидкости на криволинейные стенки.

Нахождение силы давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов. Чаще всего рассматривают цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии.

Возьмем цилиндрическую поверхность АВ с образующей, перпендикулярной к плоскости чертежа (рис. 1.15), и определим силу давления жидкости на эту поверхность в двух случаях: 1) жидкость расположена сверху (рис. 1.15, а); 2) жидкость расположена снизу (риc. 1.15, б).

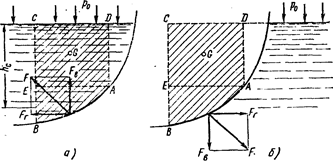
Рис. 1.15. Схема для определения силы давления

жидкости на цилиндрическую поверхность

В первом случае выделим объем жидкости, ограниченный рассмат­риваемой поверхностью АВ, вертикальными поверхностями, прове­денными через границы этого участка, и свободной поверхностью жидкости, т. е. объем ABCD, и рассмотрим условия его равновесия в вертикальном и горизонтальном направлениях. Если жидкость действует на стенку АВ с силой F, то стенка АВ действует на жид­кость с силой F, направленной в обратную сторону. На рис. 1.15 показана эта сила реакции, разложенная на две составляющие: горизонтальную F _г и вертикальную F _в.

Условие равновесия объема ABCD в вертикальном направлении имеет вид

(1.31)

где р₀ — давление на свободной поверхности жидкости; S _г — площадь гори­зонтальной проекции поверхности АВ; G — вес выделенного объема жидкости.

Условие равновесия того же объема в горизонтальном направле­нии запишем с учетом того, что силы давления жидкости на поверх­ности ЕС и AD взаимно уравновешиваются и остается лишь сила давления на площадь BE, т.е. на вертикальную проекцию поверхности Тогда

(1.32)

Определив по формулам (1.31) и (1.32) вертикальную и горизон­тальную составляющие полной силы давления F, найдем

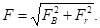
Когда жидкость расположена снизу (см. рис. 1.15, б), гидростатическое давление во всех точках поверхности АВ имеет те же зна­чения, что и в первом случае, но направление его будет противо­положным, и суммарные силы F _в и F _г определятся теми же формулами (1.31) и (1.32), но с обратным зна­ком. При этом под величиной G сле­дует понимать так же, как и в первом случае, вес жидкости в объеме ABCD, хотя этот объем и не запол­нен жидкостью.

Положение центра давления на цилиндрической стенке можно легко найти, если известны силы F _в н F _г и определены центр давления на вертикальной проекции стенки и центр тяжести выделенного объема ABCD. Задача значительно облегчается в том случае, когда рассматриваемая цилиндрическая поверхность явля­ется круговой. Равнодействующая сила при этом пересекает ось поверхности, так как любая элемен­тарная сила давления нормальна к поверхности, т. е. направлена по радиусу.

Изложенный способ определения силы давления на цилиндри­ческие поверхности применим и к сферическим поверхностям, при­чем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии.

Описанный выше прием нахождения вертикальной составляющей силы давления жидкости на криволинейную стенку используют для доказательства закона Архимеда.

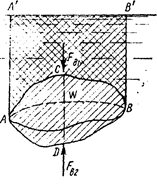
Рис. 1.16. Схема для

доказательства закона Архимеда

Пусть в жидкость погружено тело произвольной формы объемом V (рис. 1.16). Спроектируем его на свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается поверхности тела по замкнутой кривой. Эта кривая отде­ляет верхнюю часть поверхности тела АСВ от нижней ее части ADB. Вертикальная составляющая F _в1 силы избыточного давления жид­кости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме AA'B'BCA. Вертикальная составляющая F _в2 силы давления жидкости на нижнюю часть поверхности тела направ­лена вверх и равна весу жидкости в объеме AA'B'BDA. Отсюда сле­дует, что вертикальная равнодействующая сил давления жидкости на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т. е.

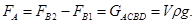
В этом и заключается закон Архимеда, обычно формулируемый так: на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости, вытесненной телом, и приложенная в центре тяжести объема погруженной части тела.

Сила F _A называется архимедовой силой, или силой поддержания, а точка ее приложения, т. е. центр тяжести объема V, — центром водоизмещения.

В зависимости от соотношения веса G тела и архимедовой силы F _A возможны три случая: 1) G > F _A — тело тонет; 2) G < F _A — тело всплывает и плавает на поверхности жидкости в частично погружен­ном состоянии; 3) G = F _А — тело плавает в полностью погруженном состоянии.

Для равновесия плавающего тела кроме равенства сил G = F _А должен быть равен нулю суммарный момент. Последнее условие со­блюдается тогда, когда центр тяжести тела лежит на одной верти­кали с центром водоизмещения. Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии заключается и следующем: центр тяжести тела должен находиться ниже центра водоизмещения. Устойчивость равновесия тел, плавающих на по­верхности жидкости, здесь не рассматривается.

Дата добавления: 2014-01-05