Равноускоренное движение сосуда с жидкостью

Прямолинейное

Ранее было рассмотрено в основном равновесие жидкости под действием лишь одной массовой силы — ее веса. Этот случай имеет место тогда, когда жидкость покоится в сосуде, неподвижном отно­сительно Земли, а также в сосуде, движущемся равномерно и прямо­линейно. Если же сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

При относительном покое свободная поверхность жидкости и про­чие поверхности уровня (см. п. 1.5) могут существенно отличаться от поверхностей уровня при покое жидкости в неподвижном сосуде, т. е. от горизонтальной плоскости. При определении формы и поло­жения свободной поверхности жидкости, находящейся в относитель­ном покое, следует руководствоваться основным свойством всякой поверхности уровня, которое заключается в следующем: равнодей­ствующая массовых сил всегда действует нормально к поверхности уровня. В самом деле, если бы равнодействующая массовая сила действовала под некоторым углом к поверхности уровня, то касатель­ная составляющая этой силы вызывала бы перемещение частиц ……..

отсутствуют какие-либо перемещения частиц жидкости как относительно стенок сосуда, так и друг относительно друга. Следовательно, единственно возможным направленном равнодействующей массовой силы является направление, нормальное к свободной поверхности, а также и к другим поверхностям уровня.

Поверхности уровня не могут между собой пересекаться,иначепо линии пересечения двух таких поверхностей был бы получен ряд точек, давление в которых в одно и то же время имело бы два разных значения, что невозможно.

Рассмотрим два характер­ных случая относительного по­коя жидкости: в сосуде, дви­жущемся прямолинейно и рав­ноускоренно и в сосуде, вра­щающемся вокруг вертикальной оси с постоянной угловой ско­ростью.

Пусть сосуд с жидкостью движется прямолинейно с по­стоянным ускорением а. В этом случае результирующую массо­вую силу, действующую на жид­кость, найдем как сумму векто­ров силы инерции, направленной в сторону, обратную ускорению а и силы тяжести (рис. 1.17).

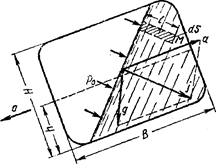Рис. 1.17. Силы, действующие при относительном

покое жидкости и прямолинейном

равноускоренном движении сосуда

Обозначив вектор равнодействующей массовой силы, отнесенной к единице массы, через 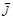, получим

где и 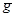— векторы единичных сил инерции и тяжести.

Для всех частиц рассматриваемого объема жидкости равнодей­ствующие массовые силы параллельны друг другу, а поверхности уровня перпендикулярны к этим силам, поэтому все поверхности уровня, в том числе свободная поверхность, являются плоскостями, параллельными друг другу. Угол наклона этих плоскостей к гори­зонту определяется из условия перпендикулярностиих к силе j.

Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно равноускоренно, необходимо к предыдущему условию добавить уравнение объемов, т. е. нужно знать объем жидкости в сосуде и выразить его через размеры сосуда В и Н и первоначальный уровень жидкости h.

Уравнение, позволяющее находить давление в любой точке рас­сматриваемого объема жидкости, можно получать аналогично тому, как это сделано в п. 1.5. Возьмем, например, около точки М пло­щадку dS, параллельную свободной поверхности, и на этой плоскости построим цилиндрический объем с образующей, нормальной к свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид

где последний член собой полную массовую силу, действующую на выделенный объем жидкости, а l — расстояние от точки М до свободной поверхности.

После сокращения на dS получим

(1-33)

В частном случае, когда а = 0 и соответственно j == g, формула (1.33.) превращается в основное уравнение гидростатики (1.20).

Tо же уравнение (1.33) можно получить интегрированием дифференциального уравнения (1.24). Для этого одну из координатных осей удобнее направить вдоль линии действия результирующей массовой силы j. Приняв такое направление, например, для оси z, будем иметь

; ; .

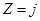Следовательно, вместо уравнения (1.24) можно записать

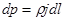
или после интегрирования и определения постоянной подстановкой параметров свободной поверхности

Полученное уравнение совпадает с формулой (1.33).

Дата добавления: 2014-01-05