Кстати:Иногда простые суждения называют атомами (атомар­ными), а сложные суждения – молекулами (молеку­лярными)

Виды суждений:

1 Атрибутивные (от лат. atributum – предназначенное, наделенное)

Выражают принадлежность (не принадлежность) того или иного свой­ства предмету. Также называются категорическими

(от лат. categorikos – ясный, безусловный, не допускающий иных толкований).

Логическая схема суждения: S – P (S₁, S₂, S₃, – P), (S – P₁, P₂, P₃)

2 Реляционные (от лат. relativus – относительный)

Выражают различные отношения между предметами, понятиями о предметах и пр.

Логическая схема суждения: x R y (x, y – члены отношения)

3 Экзистенциальные (от лат. existentia – существование)

В них выражается сам факт существования или не существования предмета суждения.

Большинство суждений – категорические. Среди них существует разделение по количеству: на единичные, общие и частные; по качеству: на утвердительные и отрицательные.

Например: Все S есть P

Некоторые S есть P

По крайней мере некоторые S есть P

Слова «все», «некоторые» и другие подобные слова, которые характе­ризуют суждение со стороны его количества, называются кванторными слова­ми (от лат. quantum – сколько). Операция введения таких слов в суждение назы­вается квантификацией, а операторы – кванторами.

Различают

квантор общности: " (все, каждый, всегда….)

квантор существования: $ (некоторый, иногда, бывает, существует…)

Объединенная классификация суждений:

Общеутвердительные: «Все S есть P»

Общеотрицательные: «Ни один S не есть P»

Частноутвердительные: «Некоторые S есть P»

Частноотрицательные: «Некоторые S не есть P»

Утвердительные суждения обозначаются двумя первыми гласными буквами латинского слова affirmo – утверждаю; а отрицательные – слова nego – отрицаю.

С помощью кругов Эйлера это выглядит так:

А Общеутвердительные:

«Все бамбуки есть злаки»

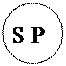
«Все квадраты – равносторонние прямоугольники»

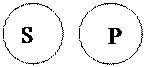Е Общеотрицательные:

«Ни один герой не является трусом»

I Частноутвердительные:

«Некоторые математики были астрономами»

«Некоторые орудия – ракетные»

О Частноотрицательные:

«Некоторые водные животные не есть позвоночные»

«Некоторые языки не имеют форм склонения»

Распределенность того или иного термина в суждениях.

Термин считается распределенным, если взят в полном объеме. Иначе – нераспределен.

Суждения	S	P
A	+	–
A	+	+
I	–	–
I	–	+
E	+	+
O	–	+
O	–	+

В общем случае руководствуются правилом:

1 Субъект S считается распределенным в общих суждениях (общеутверди­тельных и общеотрицательных) и нераспределен в частных суждениях (частноутвер­дительных и частноотрицательных)

2 Предикат Р распределен во всех отрицательных и в тех частноутверди­тельных суждениях, в которых Р подчинен S. Предикат нераспределен в обще­утвер­дительном (за исключением дефиниции) и в тех суждениях, в которых S и Р перекрещивающиеся понятия.

Операции с суждениями

Установление точного логического смысла суждений

Далеко не всегда точный логический смысл суждения оказывается ясным и прозрачным для мысли. Чтобы избежать противоречий, неясности, чтобы иметь возможность проанализировать то или иное суждение, необходимо установить точный логический смысл суждения, т.е. преобразовать форму выражения таким образом, чтобы ясно могли быть определены S, Р и связка между ними.

Например: “В еловых лесах живет мало певчих птиц”. Для логического анализа такая форма не совсем удобна. Преобразовав предложение в: “Все еловые леса принадлежат к лесам с малочисленным населением певчих птиц”, мы придаем суждению форму, которая, не меняя его логического смысла, делает более явным положение S, Р и связки.

Обращение

Преобразование, при котором Р становится S, а S – Р, но логическое содержание остается тем же самым.

Например: “Все пешеходы – участники дорожного движения”. При обра­щении получаем: “Некоторые участники дорожного движения – пешеходы”.

Обращение делает для нас более отчетливым количество S и Р, а также отношение между их объемами в суждении. В самом деле:

S – пешеходы

Р – участники дорожного движения

Превращение

Если в операции обращения мы «работаем» с Р, то в операции превращения мы «переключаем внимание» на S. При превращении рассматривается отношение субъекта не просто к Р исходного суждения, но к понятию, противоречащему Р.

До превращения: S – Р. После превращения: S – не-Р

Противопоставление предикату

Основывается на том, что каждое понятие может мыслиться не только в своем собственном положительном содержании, но и по отношению к противо­речащему ему понятию. Противопоставление предикату есть высказывание не о предикате суждения, а о понятии, противоречащем понятию предиката.

Противопоставление предикату является соединением превращения с обращением. Чтобы произвести противопоставление, сначала производится превращение, а затем превращенное суждение обращается.

Сопоставление суждений по логическому квадрату

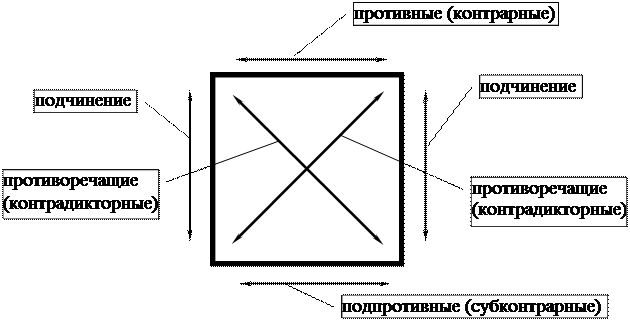Дата добавления: 2014-01-05