Вектор ускорения

Ускорение характеризует темп изменения скорости. Как и ранее, вводится понятие среднего ускорения и в случае 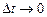имеем величину, характеризующую мгновенное ускорение:

.

Размерность ускорения .

Соответствующие компоненты ускорения в Декартовой системе координат могут быть представлены в виде:

, , .

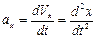В случае прямолинейного движения вектор ускорения направлен параллельно вектору скорости. Движение может быть ускоренным или замедленным. Ускорение может быть постоянной величиной (равноускоренное или равнозамедленное движение) или переменной.

В случае криволинейного движения всегда существует ускорение, определяющее изменение скорости как векторной величины, нормальное ускорение (). Если движение вдоль траектории неравномерно, то есть и тангенциальное ускорения (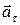). Нормальное ускорение всегда направлено вдоль радиуса кривизны траектории движения тела, в направлении изменения скорости как векторной величины, и называется центростремительным ускорением.

, ,

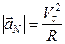где 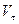- тангенциальная скорость движения тела (скорость вдоль траектории движения), 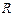- радиус кривизны траектории.

В случае равномерного движения тела (материальной точки) по окружности, .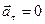

Размерность ускорения: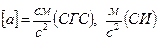

Ниже представлена таблица первых производных и неопределенных интегралов от некоторых элементарных функций, знание которых необходимо для понимания излагаемого далее материала.

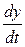
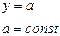
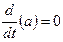
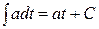
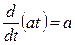
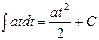
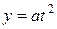
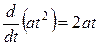
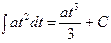
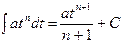
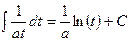
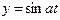
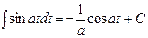
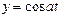
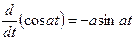
где С = const и называется константой интегрирования. При решении задач она определяется какими-либо граничными условиям.

Производная по от произведения двух функций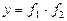

Производная по от отношения двух функций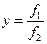

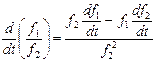
Пример: определение зависимостей скорости прямолинейного движения и пройденного материальной точкой пути от времени при равноускоренном (равнозамедленном) движении (

По определению, мгновенное значение ускорения определяется выражением:

,

которое представим в виде: 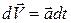. Интегрируем это уравнение 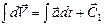и получаем: 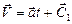, где 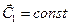. Найдем ее значение. Предположим, что в начальный момент времени скорость тела была равной 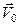. Подстановка этого условия в полученное выражение для скорости движения тела приводит к соотношению Поэтому имеем:

.

Для нахождения зависимости пройденного телом пути от времени воспользуемся определением мгновенной скорости: и полученной зависимостью ее от времени в условиях неизменности величины ускорения. Так как 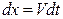,имеем: 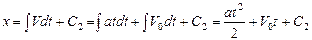, где .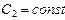

Как и ранее, определим постоянную интегрирования через начальные условия. Если в начальный момент времени координата тела была равной , то получаем: и зависимость координаты тела от времени принимает вид:

.

Дата добавления: 2014-01-05