Масса. Количество движения. Сила. Второй закон Ньютона. Третий закон Ньютона

Инерциальные системы отсчета. Первый закон Ньютона

Основы динамики.

В предыдущих разделах изучалось движение тел (материальной точки), вне зависимости от причин вызывающих его. Динамика, это раздел механики, в котором изучаются характеристиками движения тел в зависимости от сил, действующих на эти тела.

Рассмотрим тело, находящееся столько далеко от других тел, что оно не испытывает их воздействие. Такое тело называется свободно движущимся. Конечно, в природе таких тел нет, однако предположить это, в рамках классической физики, мы можем.

Свободное движение, как и всякое другое, выглядит по-разному в различных системах отсчета. Однако, если выбрать в качестве тела отсчета другое свободно движущееся тело, то относительно него свободное движение других тел будет выглядеть наиболее просто - движение будет прямолинейным и равномерным.

Система отсчета, связанная со свободно движущимся

телом, называется инерциальной системой отсчета.

Свободное движение тел в инерциальной системе отсчета всегда прямолинейно и равномерно.

Этот закон инерции был впервые сформулирован Галилеем (1632г.). Закон инерции также называется первым законом Ньютона.

Все физические явления, за редким исключением, изучают в инерциальных системах, которые, фактически, являются таковыми только приблизительно. Система отсчета связанная с Землей не является инерциальной, о чем свидетельствует изменения плоскости колебаний маятника с течением времени (маятник Фуко).

В 1687 году Ньютон опубликовал свой фундаментальный труд «Математические начала натуральной философии», в котором впервые отчетливо было введено понятие «масса» и указано на то, что масса и вес существенно разные физические характеристики.

В соответствии с представлениями Ньютона, под массой (m) будем понимать величину, характеризующую:

- количество материи в теле,

- меру инертности тела и

- являющуюся объектом и источником тяготения.

Масса измеряется в граммах (система СГС) или в килограммах (интернациональная система, СИ). Эталон единицы массы хранится в палате мер и весов в Париже.

Количеством движения в физике называют векторную величину, равную произведению массы тела на скорость его движения:

Если тело совершает свободное движение, то его количество движения не меняется. Если же на тело оказывают действие другие тела, то его величина меняется и поэтому изменение количества движения можно рассматривать как меру воздействия на данное тело других тел.

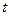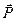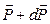Предположим, что в момент времени тело имело количество движения , а в момент времени , его величина стала . Изменение количества движения за промежуток времени 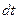составляет 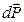. Величина характеризует скорость изменения количества движения и называется силой. называется силой ().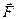

Изменение количества движения пропорционально приложенной движущей силе и происходит в направлении действия этой силы.

.

Это равенство называется уравнением движения и является отображением второго закона Ньютона.

Если масса тела величина постоянная, то

Если известно поле действия сил, зависимость 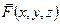, координаты положения и скорость тела в некоторый момент времени, то уравнение движения позволяет вычислить координаты, скорость и ускорение материальной точки в любой момент времени. Компоненты вектора силы в Декартовой системе координат определяют характер движения материальной точки по соответствующим направлениям:

, ,

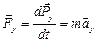Третий закон Ньютона устанавливает характер взаимодействия между телами, действующими друг на друга:

действия двух тел друг на друга всегда равны и противоположно направлены.

Примера: с какой силой тело действует на подставку, с такой же силой, но противоположно направленной, подставка действует на тело.

Задача.

Тело брошено в поле тяжести Земли с начальной скоростью под углом 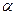к горизонту. Определить максимальную высоту подъема тела и дальность его полета.

Для решения этой задачи выберем в качестве тела отсчета Землю, а систему координат расположим таким образом, что движение будет происходить в плоскости 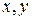из точки с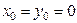

В выбранной системе отсчета, компоненты начальной скорости в направлениях 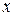и 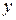имеют вид

,

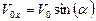Так как вдоль оси 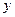на тело не действует сила, движение вдоль нее будет равномерным и происходить со скоростью 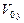, при этом положение тела на этой оси будет определяться выражением . При этом, дальность полета тела () зависит от времени полета ():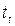

.

Движение тела вдоль оси 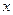осложнено действием силы тяжести, направленной в сторону, противоположную направлению начальной скорости . Предполагая, что ускорение свободного падения (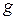) не зависит от высоты подъема тела, из уравнения с учетом того, что в точке максимального подъема 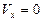определим время подъема ()

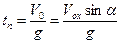
и высоту

.

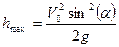Основываясь на том, что время подъема и время падения тела равны, а при данной постановке задачи это так и есть (диссипативные силы отсутствуют), находим, что время полета тела равно:

.

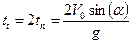Следовательно, максимальная дальность полета тела определяется выражением:

.

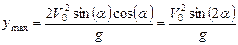Из полученного выражения видно, что при угле дальность полета тела будет максимальной из возможных для данной начальной его скорости и что дальность полета тела одинакова при углах 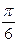и .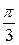

Дата добавления: 2014-01-05