Силы инерции

До сих пор движение тел изучалось в инерциальных системах отсчета. Однако, в реальности все физические системы отсчета неинерциальны, т.е. движутся с ускорением. В таких системах, с точки зрения наблюдателя, движущегося вместе с системой, возникают дополнительные силы, называемые силами инерции. Характерной общей особенностью этих сил является их пропорциональность массе тела, на которое они действуют. Это свойство делает их аналогичными силам тяготения.

Широким классом неинерциальных систем являются вращающиеся системы отсчета, в частности, к ним относится Земля.

Рассмотри простейший случай: равномерно вращающийся с угловой скорость 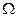диск (радиус диска 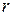) и, равномерно движущуюся вдоль края диска, частицу (масса частицы 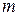). Пусть скорость частицы относительно диска равна 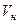(индекс «н» означает, что эта скорость в неинерциальной системе отсчета). Тогда относительно неподвижного наблюдателя, находящегося вне диска (инерциальная система отсчета), скорость частицы будет 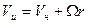. В инерциальной системе отсчета ускорение, с которым движется частица, определяется выражением:

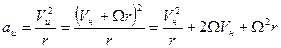
Следовательно

С другой стороны, с точки зрения наблюдателя, находящегося на диске, т.е. для которого диск неподвижен, на тело действует только одна (центростремительная) сила:

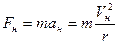
Сравнение и

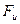
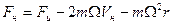
показывает, что для наблюдателя находящегося на диске на частицу кроме «истинной силы» действуют еще две:

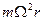-- центробежная сила и

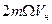-- сила Кориолиса.

Знак минус показывает, что эти силы направлены от оси вращения диска.

Центробежная сила на экваторе уменьшает вес на 0,3%. В специальных центрифугах она может создавать значительные перегрузки.

Сила Кориолиса существенно отличается от центробежной. Она действует только на тела, движущиеся относительно вращающейся системы отсчета. Особенностью этой силы является то, что она не зависит от положения тела, а только от его скорости в этой системе. Сила Кориолиса направлена перпендикулярно скорости 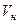. В векторной форме она записывается в виде: 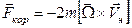Сила Кориолиса не совершает работы над телом в направлении его движения, а только изменяет направление скорости его движения.

3. Механические колебания и волны

3.1. Гармонические колебания

Наряду с поступательным и вращательным движениями имеется еще один широкий класс механического движения – колебательное движение.

Периодическим колебательным движением является такое движение, при котором через равные промежутки времени (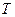) частица (тело) имеет одно и то же положение, одну и ту же скорость и ускорение. 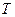называется периодом колебаний. Если в некоторый момент времени 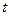координата скорость и ускорение частицы известны, то через промежуток времени кратный периоду колебаний они будут такими же. Величина обратная периоду колебаний называется частотой колебаний 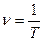. Частота колебаний показывает сколько раз в 1 сек повторяются характеристики движения. 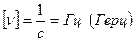. Существует бесчисленное множество типов периодических движений. Простейшими из них (с точки зрения математического анализа) являются гармонические колебания. Это такие колебания, при которых положение частицы в пространстве меняется по гармоническому закону:

,

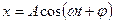где 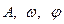постоянные величины, которые имеют простой физический смысл:

- амплитуда колебаний - максимальное отклонение частицы от положения . .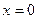

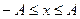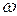- частота колебаний. [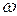] = 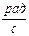. Так как период гармонической функции равен 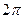, то, следовательно, 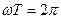. Поэтому .

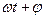() - фаза колебаний.

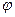- начальная фаза колебаний.

Покажем, что гармонические колебания могут быть записаны в виде:

,

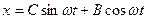причем, эта форма записи эквивалентна предыдущей:

.

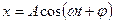Для этого воспользуемся утверждением, что если эти выражения эквивалентны, то значения 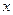и 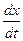вычисляемые с их помощью должны быть равны в любой момент времени. Из условия равенства значений 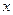в момент времени 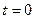получаем:

Дата добавления: 2014-01-05