Начальными условиями движения

Связь амплитуды гармонических колебаний с

Амплитуда гармонических колебаний определяется только начальными условиями: либо начальным смещением относительно точки равновесия (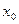), либо начальной скоростью (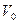), либо и тем и другим параметром. Покажем это.

Пусть 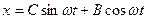. Если при 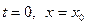то получаем:

.

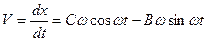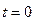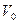Если скорость при равна , то

.

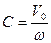Итак, уравнение гармонических колебаний с учетом начальных условий имеет вид:

.

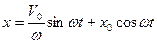При этом амплитуда колебаний:

.

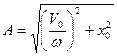Если в процессе колебательного движения на тело не действуют силы, изменяющие амплитуду колебаний, то такие колебания называются свободными, а частота, на которой они происходят – собственной.

Определим силу, которая может привести к возникновению гармонических колебаний. Для этого умножим полученное выражение для ускорения на массу тела, совершающего колебательное движение. Получим:

Итак, тело совершает гармоническое колебательное движение, если действующая сила пропорциональна смещению и имеет обратный знак. Примером такой силы может служить сила упругости, возникающая при малых (упругих) деформациях различных тел. Эта сила называется восстанавливающей. Такая зависимость силы от координаты часто встречается при решении различных задач, например: задачи о движении шарика в потенциальной яме, о колебаниях маятник и т.д. В общем случае, абсолютно линейной зависимости между восстанавливающей силой и смещением не может быть, однако, если смешения достаточно малы, то такая зависимость достаточно хорошо описывает движение системы. Колебания с малой амплитудой почти всегда можно считать гармоническими.

Выражение может быть представлено в ви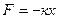де: , где 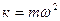и называется коэффициентом жесткости.

Дата добавления: 2014-01-05