Математический маятник

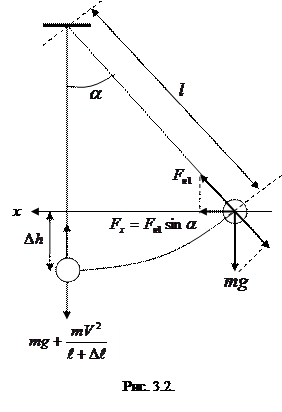
Математический маятник состоит из подвешенной на невесомой нерастяжимой нити материальной точки, которая может совершать колебательное движение в поле действия гравитационных сил или в поле действия сил инерции.

Для того, что бы реализовать эту модель на практике должны выполняться следующие условия:

1. размер тела должен быть много меньше длины нити ,
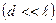2. масса тела должна быть много больше массы нити ,
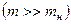3. происходящее во время колебаний изменение длины нити должно быть много меньше длины самой нити 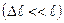. Остановимся на последнем более подробно.

При максимальном отклонении маятника от состояния равновесия сила натяжения нити 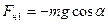, где 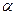- угол максимального отклонения. При прохождении телом положения равновесия сила натяжения нити определяется как силой тяжести, так и центробежной силой 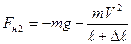, где величина центробежной силы может быть найдена следующим образом. Согласно закону сохранения энергии запишем

,

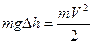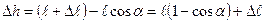
откуда следует:

.

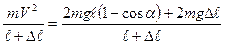Итак, величина 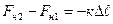определяет значение 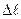, которое должно быть много меньше 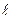. Расчет показывает, что это условие выполняется, когда

.

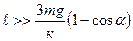Из полученного выражения следует, что подбором амплитуды колебаний (угла максимального отклонения) это условие может быть всегда выполнено.

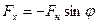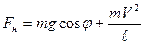Теперь рассмотрим движение самого маятника. Возвращающая сила, действующая вдоль оси «х» определяется силой натяжения нити , где , а 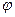-угол отклонения 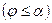. Воспользуемся законом сохранения энергии и получим выражение для центростремительной силы

,

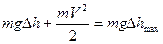где 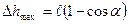соответствует отклонению маятника на максимальный угол 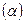, а .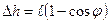

После подстановки соответствующих величин в выражение для получим:

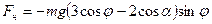
Если угол отклонения маятника настолько мал, ч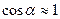то , то

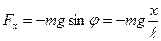
Сравнивая это выражение с выражением для силы, определяющей гармонические колебания, видим, что частота колебаний математического маятника

,

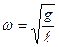а период колебаний составляет величину:

.

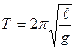Период колебаний математического маятника зависит от его длины и от характеристики поля, в котором он находится.

Дата добавления: 2014-01-05