Физический маятник

Физическим маятником называется твердое тело, способное совершать колебательное движение в поле действия гравитационных сил или сил инерции (см. рис. 3.3).

Ранее было показано, что законы вращательного движения тела формально не отличаются от законов движения материальной точки, с той разницей, что производится замена величин , , .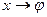

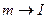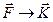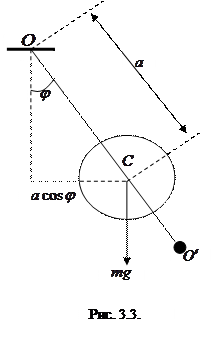В данном случае (см. рисунок) момент силы действующий на физический маятник равен:

.

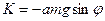Если амплитуда колебаний мала, то и углы отклонения маятника от состояния равновесия (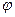) малы, поэтому 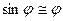. В этом случае можем записать: 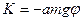. Видим, что 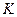~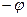и что в рассматриваемом случае роль коэффициента жесткости играет величина .

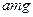По аналогии с выражением 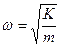можно написать выражение для частоты колебаний физического маятника в виде:

.

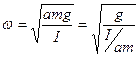Замечание. Если в полученное выражение для частоты колебания физического маятника подставить значение момента инерции, соответствующее материальной точке находящейся на расстоянии 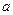от точки подвеса (), то полученное выражение будет соответствовать частоте колебаний математического маятника, длиной .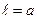

Сравнивая формулу для частоты колебаний физического маятника, с соответствующей формулой для математического маятника 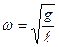, мы видим, что частота колебаний физического маятника будет равна частоте колебаний математического, если его длина будет составлять величину

.

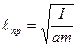Это, так называемая, приведенная длина физического маятника. Так как 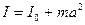, где 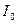- момент инерции тела относительно оси, проходящей через центр инерции 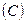, выражение для приведенной длины мы можем записать в виде:

.

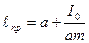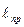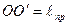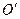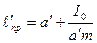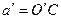Из этого выражения следует, что периоды колебаний физического маятника, подвешенного на параллельных осях, отстоящих друг от друга на расстояние равны. В самом деле, отложим на прямой ОС отрезок . Подвесим маятник на ось, проходящую через точку . Тогда приведенная длина будет , где . Но 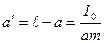. Подставим это в выражение для и получим:

.

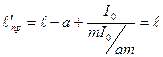Итак: приведенные длины, а значит и периоды (частоты) колебаний физических маятников, подвешенных на параллельных осях, отстоящих друг от друга на величину равную приведенной длине равны.

Дата добавления: 2014-01-05