Затухающие колебания

До сих пор рассматривались незатухающие колебания. Но если колебательное движение тела происходит в среде (жидкость, газ), которая препятствует движению, то энергия колебаний будет переходить в тепловое движение молекул, т.е. будет иметь место диссипация энергии.

При малых скоростях движения тел в газах и жидкостях сила трения () пропорциональна скорости движения тела – этосила вязкого трения Стокса (об этой силе более подробно будет говориться позже):

,

где 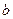- некоторая константа, определяемая характеристиками среды и параметрами тела.

Выясним, как влияет сила трения на колебательное движение. Будем считать, что сила трения настолько мала, что за время, равное одному периоду, амплитуда колебаний практически не меняется, т.е. изменение амплитуды колебаний много меньше самой амплитуды.

Очевидно, энергия, теряемая совершающим колебание телом, равна работе силы трения. За время 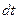эта работа составляет величину:

.

Это уравнение может быть представлено в виде:

.

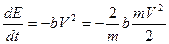Ранее было сделано предположение, что изменение амплитуды колебаний, а, следовательно, и энергии, за время, равное периоду колебаний, очень мало. Поэтому вместо кинетической энергии можно записать в последнем уравнении среднее за период значение полной энергии (E), . В результате получим:

.

Введем обозначение и перепишем последнее выражение в виде:

или .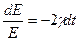

Но , поэтому:

.

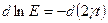Интегрируя, получаем:

.

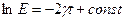Теперь предположим, что в начальный момент времени 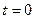полная энергия колебаний была равной . Это предположение позволяет определить константу, которая оказывается равной 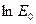. В результате имеем выражение:

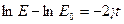или ,

из которого следует:

.

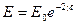Видим, что энергия колебаний убывает по экспоненциальному закону. При этом, т.к. 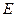~изменение амплитуды колебаний во времени имеет вид:

.

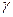- называется коэффициентом затухания.

Из полученной зависимости видно, что за время 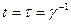амплитуда колебаний убывает в 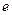раз.

.

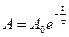Это время называется временем затухания.

Из ранее сделанного предположения относительно незначительной потери энергии за период колебания, следует, что . Значит, за время система совершит колебаний. Величина называется логарифмическим декрементом колебаний.

Вид затухающих колебаний представлен на рис. 3.4.

Необходимо отметить, что затухающие колебания не являются гармоническими.

Если сила трения велика на столько, что существенное изменение амплитуды происходит за время меньшее чем период колебания, то такие колебания называются апериодическими.

Дата добавления: 2014-01-05