Вынужденные колебания

В реальных условиях колебания механических систем всегда являются затухающими. Для создания незатухающих колебаний нужно подводить энергию из вне с помощью действия внешних сил. Колебания, совершаемые в результате действия внешней силы, называются вынужденными. Простейшим, с точки зрения математического анализа, случаем является случай, когда внешняя сила меняется по гармоническому закону:

.

Здесь - частота действия внешней силы, собственную частоту колебаний системы будем теперь обозначать .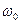

Запишем уравнение движения в виде:

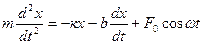
и трансформируем его с учетом обозначений введенных ранее:

.

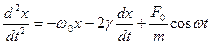Решение уравнения будем искать на частоте внешней силы, т.е. предположим, что решение уравнения имеет вид:

.

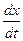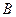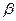Далее найдем значения и , подставим их в исходное уравнение, из которого в последствии исключим время. Получим два уравнения с двумя неизвестными и . Определим их и проанализируем полученные выражения.

Итак:

,

,

.

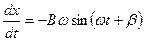Подставим эти выражения в уравнение движения и получим:

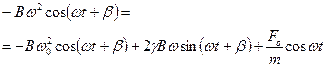
или

.

Теперь воспользуемся известными соотношениями:

,

,

которые позволяют преобразовать наше уравнение к виду:

Теперь воспользуемся тем, что искомое решение должно быть справедливым в любой момент времени, поэтому запишем полученное выражение для моментов времени, когда 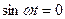и когда . Получим два уравнения, не содержащие время

,

которые позволяют определить искомые коэффициенты 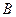и .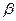

,

.

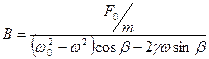Воспользуемся последним из представленных выражений и найдем 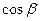и :

,

,

и 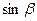определим 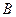. В результате проведенных вычислений получим:

.

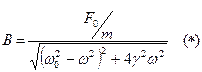
Проведем краткий анализ этих выражений.

Рассмотрим фазовый сдвиг 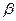. При 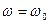величина . Видим, что скорость совершающего колебания тела

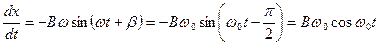
всегда находится в фазе с внешней силой , внешняя сила всегда направлена вдоль скорости и всегда ускоряет тело. Условие 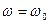соответствует условию максимальной передачи энергии от внешней силы в колебательную систему. Это условие резонансного взаимодействия, условие резонанса. Если 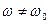, то часть времени внешняя сила ускоряет тело, а часть времени замедляет.

В условиях резонансного взаимодействия (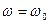) амплитуда колебаний имеет максимальную величину, равную:

.

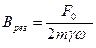Теперь перепишем выражение для амплитуды вынужденных колебаний () в виде:

и преобразуем его

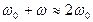Предполагая, что , можем записать . С учетом этого имеем:

,

Теперь, используя последнее выражение, построим график зависимости амплитуды вынужденных колебаний от частоты внешней силы (см. рис. 3.5), который называется резонансной кривой. Ширина резонансной кривой определяется коэффициентом затухания 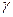. Чем больше коэффициент затухания, тем шире резонансная кривая. Если , то резонансная кривая представляет собой -функцию.

Дата добавления: 2014-01-05